1、※1选择题:点p(8,-66)在平面直角坐标系所在的象限为( )。A.第一象限 B.第二象限 C.第三象限 D.第四象限解题思路:根据直角坐标系内任意点P(a,b)横坐标和纵坐标的符号关系可知,当a>0,b>0时,点p在第一象限内;当a<0,b>0时,点p在第二象限内;a<0,b<0时,点p在第三象限内;a>0,b<0时,点p在第四象限内。对于本题,因为8>0,-66<0,所以该点p(8,-66)在第四象限内,故选择答案D。

2、※2选择题:点(84,-96)到y轴的距离是( )。A. 84 B. 96 C.-96 D.- 84解题思路:本题考察的距离知识点,因距离为非负数,所以答案C和D可以排除,又因为本题是求点到y轴的距离,即距离为点的横坐标的绝对值,由于横坐标为84>0,所以本题点(84,-96)到y轴的距离是84,即选择A.

3、一次函数,也称为线性函数,是一种形式为 y = ax + b 的函数,其中 a 和 b 是常数,且 a ≠ 0。这意味着 y 与 x 之间的关系是线性的,即它们的图像是一条直线。
4、※4填空题:点(51b-21, 9b+1)在y轴上,则点的坐标为 。解题过程:因为点在y轴上,所以横坐标为0,即有51b-21=0,可求出b=7/17,进一步代入纵坐标有:9b+1=9*7/17+1=80/17,则本题所求点的坐标为:(0, 80/17)。※5填空题:若一次函数y=6x+b经过点(6,-8),则b= 。解题步骤:因为一次函数y=6x+b经过点(6,-8),即点的坐标满足直线方程,代入有:-8=6*6+b,则b=-8-6*6=-8-36=-44,即为本题所求的值。

5、※6填空题:已知一次函数y=6x+63-9m.(1)若函数图像与y轴的交点在位于y轴的负半轴,则m的取值范围为 ;(2)若-27≤x≤13,函数y的最大值为132,则m的值为 。解题步骤:(1)一次函数y=6x+63-9m与y轴的交点在y轴的负半轴,即x=0处时,有函数值y<0,即:6*0+63-9m<0,则9m>63,所以m>7。(2)一次函数的单调性取决于自变量系数,对于一次函数y=ax+b,当系数a为正数时,函数y为增函数,当系数a为负数时,函数y为减函数。对于本题a=6>0,故本题一次函数y=6x+63-9m为增函数,则函数最大值在x取到最大值时达到,所以:6*13+63-9m=132,即9m=9,则m=1.

6、7计算题:一次函数经过点A(-31, 27),B(45, 33)两点,求函数的表达式。解:方法一:方程计算法设该一次函数表达式为y=kx+b,根据题意两点在图像上,则有方程:27=-31k+b;33=45k+b.两方程相减有:33-27=(45+31)k,则k=3/38.代入其中一个方程有:33=3/38*45+b,即可求出b=1119/38,所以一次方程的表达式为:y=3x/38+1119/38。方法二:直线方程点斜式计算根据题意,图像经过A,B两点,则该直线的斜率k为:k=(33-27)/[45-(-31)]=3/38.则直线的方程为:y-27=3/38(x+31)。

7、8计算题:已知函数y-5与8x+81成正比例,且当x=-7时,y=6。(1)求y与x的函数关系式。(2)求函数y与两坐标轴围成的面积。解:(1)根据题意,设比例系数为k,有:y-5=k(8x+81),将点x=-7,y=6代入有:6-5=k(-8*7+81),即k=1/25,此时函数关系式为:y-5=1/25(8x+81),即y=8x/25+206/25.
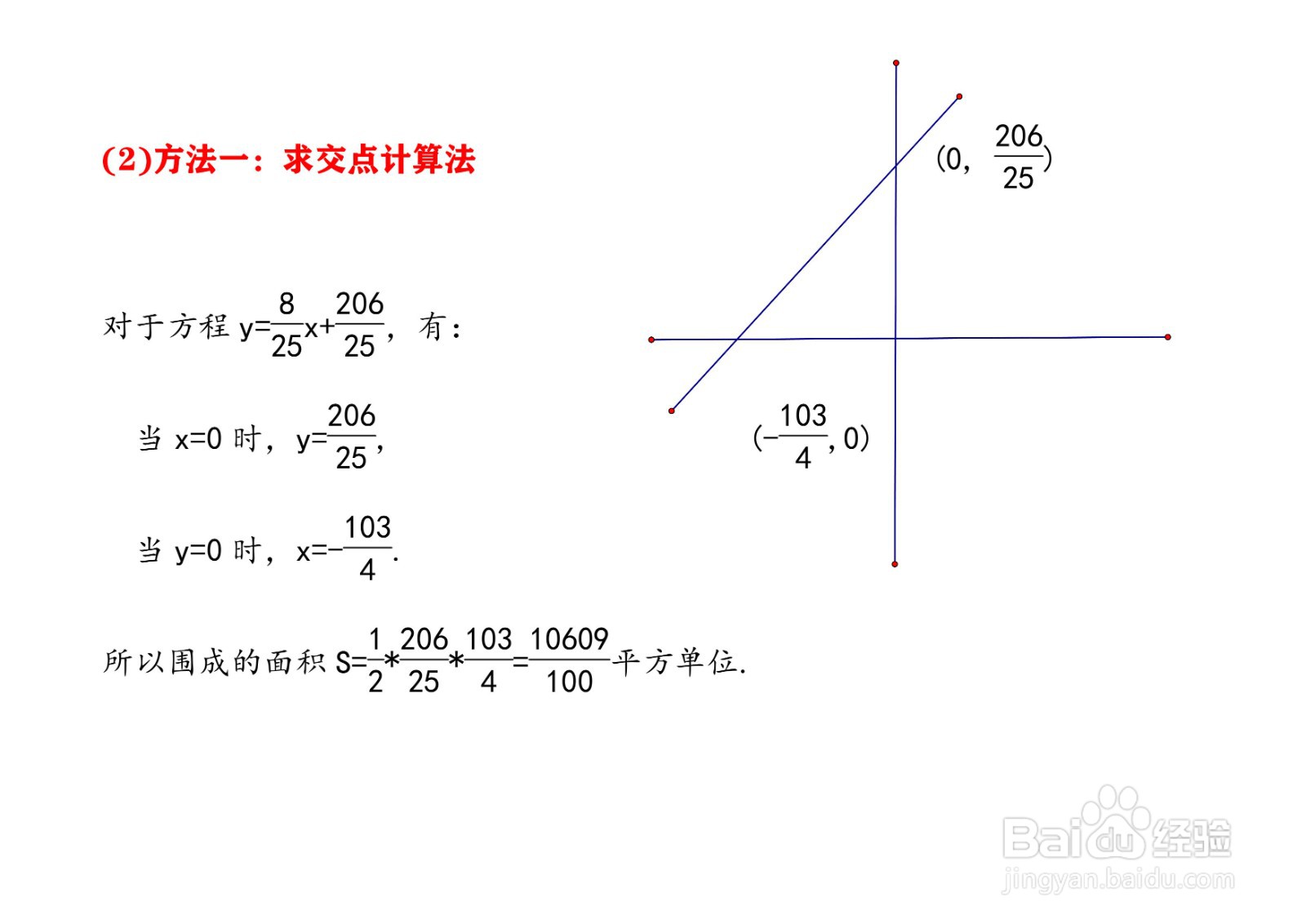

8、(2)方法一:求交点计算法对于方程y=8x/25+206/25,有:当x=0时,y=206/25,当y=0时,x=-103/4.所以围成的面积S=(1/2)* 206/25*103/4=10609/100平方单位.
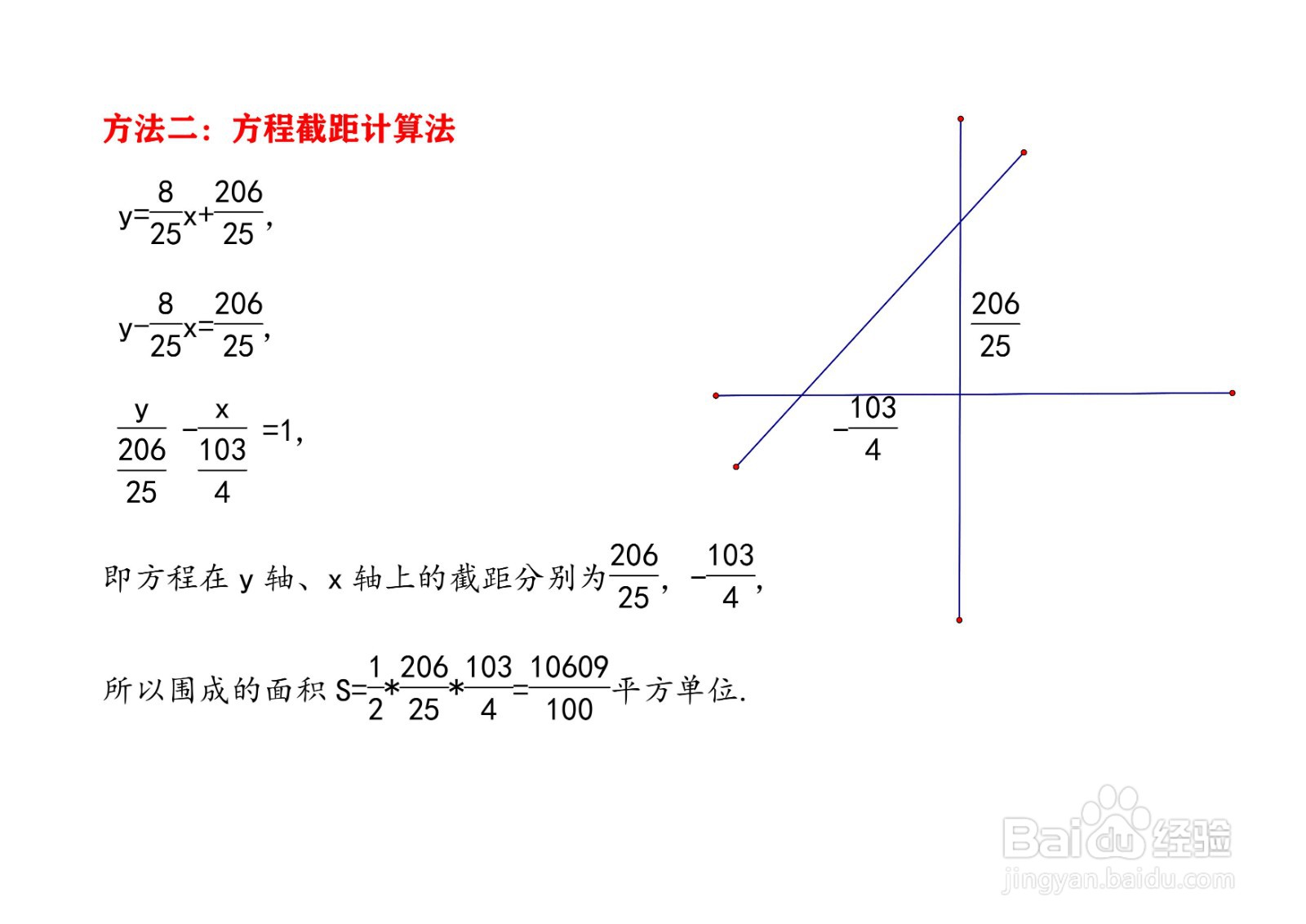
9、方法二:方程截距计算法y=8x/25+206/25,y-8x/25=206/25,y/(206/25)-x/103/4=1,即方程在y轴、x轴上的截距分别为206/25,-103/4,所以围成的面积S=(1/2)* 206/25*103/4=10609/100平方单位.
10、一次函数的解析式具有以下特点:图像是一条直线,且斜率为 a。斜率k是直线倾斜程度的度量,其值等于直线与 x 轴正方向之间的角度的正切值。在一次函数中,斜率 a 决定了直线的倾斜程度。直线在 y 轴上的截距为 b。截距是直线与 y 轴交点的纵坐标。在一次函数中,截距 b 表示当 x = 0 时,y 的值。一次函数具有单调性。也就是说,无论 x 值如何变化,y 值总是按照一定的趋势(增加或减少)变化。当 a > 0 时,函数在定义域内单调递增;当 a < 0 时,函数在定义域内单调递减。