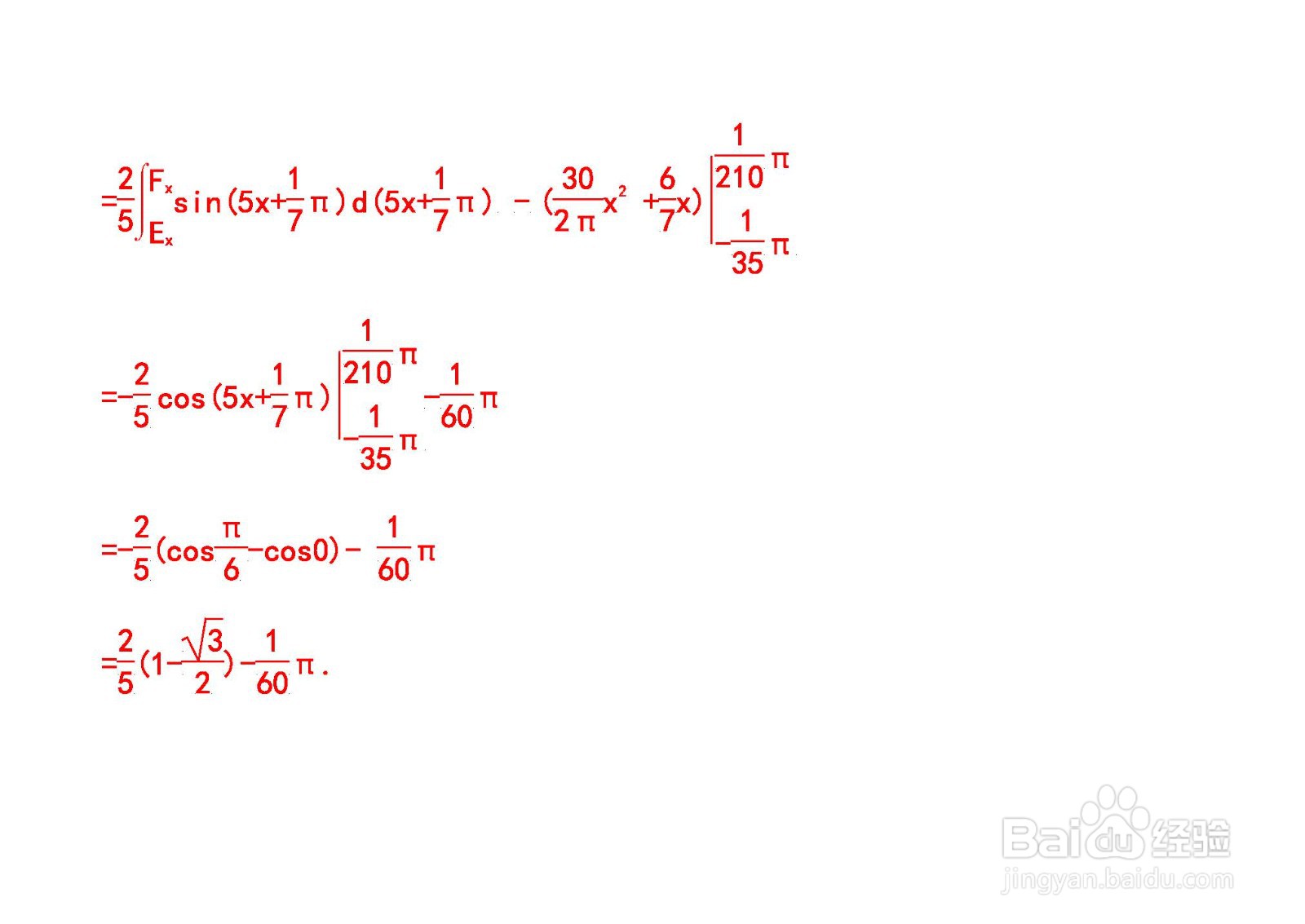1、解析该函数的定义域、值域、最小正周期、对称轴等性质。
2、f(x)是函数的符号(y),f代表法则,y它代表函数图像上每一个点的纵坐标的数值,因此函数图像上所有点的纵坐标构成一个集合,这个集合就是函数的值域。

3、该正弦三角函数的对称中心计算解答:
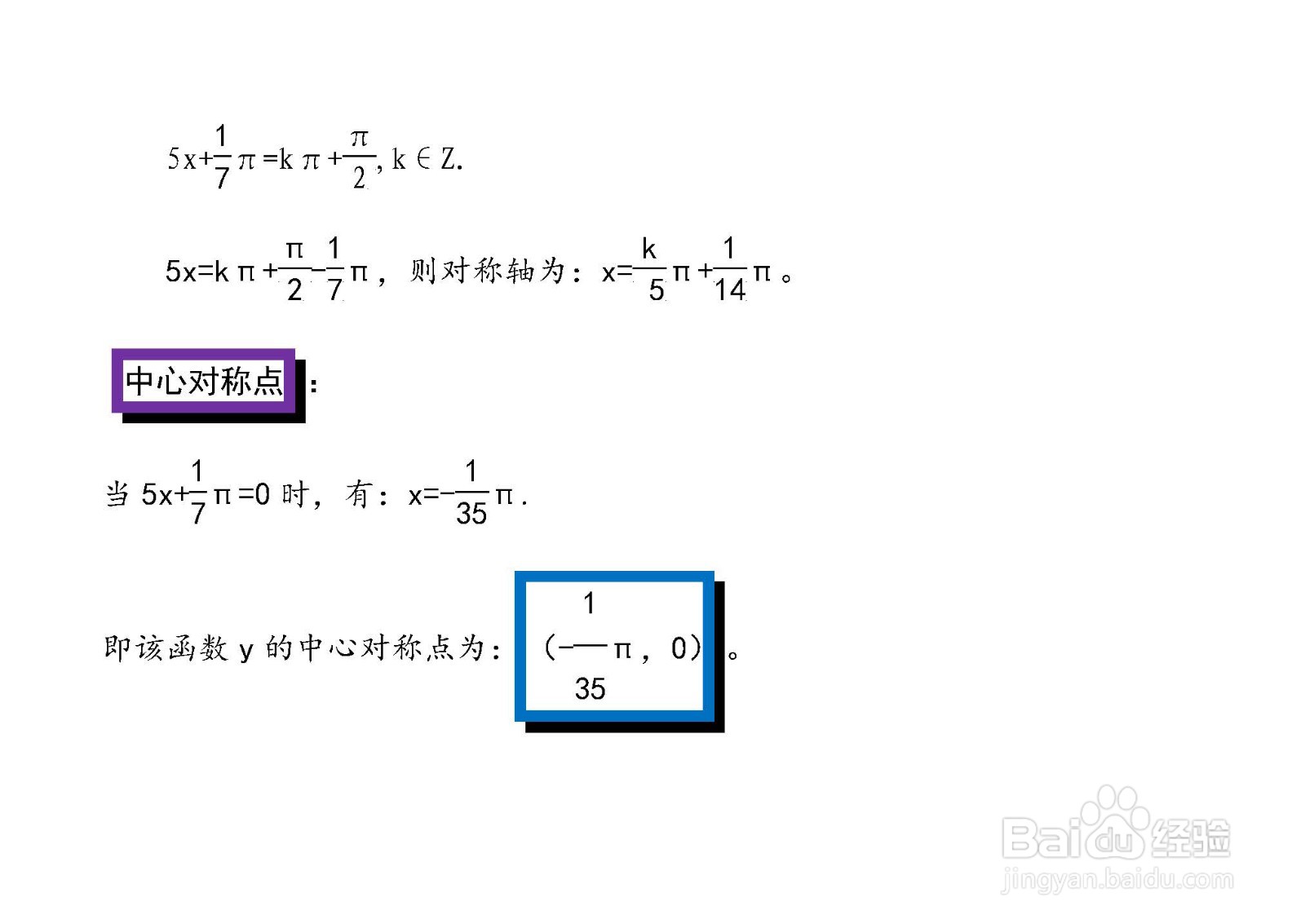
4、该正弦复合函数的一阶、二阶和n阶导数计算详细过程。

5、函数的单调增区间解析。

6、函数的单调减区间解析。

7、函数的一阶导数应用,计算曲线上定点的切线方程,本例以曲线上的某两个点切线方程计算。

8、函数一阶导数的几何意义是切线斜率。具体来说,一个函数在某一点处的导数值代表了该点处函数图像切线的斜率。当一阶导数值大于0时,表示函数在该点处是递增的,当一阶导数值小于0时,表示函数在该点处是递减的。

9、定积分知识运用,计算图像半个周期内与x轴围成的面积的步骤。

10、介绍直线与正弦函数y围成区域的面积的详细计算过程。

11、进一步对定积分进行化简计算,得到直线与函数围成区域的面积。