1、函数y=x^3+2x^2+x为幂函数的四则运算,自变量x可以取全体实数。
2、计算函数的一阶导数,根据导数的符号,判断函数的单调性,并计算函数y=x^3+2x^2+x的单调区间。
3、解析函数的凸凹性,计算函数的二阶导数,根据导数的符号,判断函数的凸凹性质并计算函数y=x^3+2x^2+x的凸凹区间。
4、如果函数f(x)在区间I上二阶可导,则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
5、解析函数在无穷处的极限,即函数y=x^3+2x^2+x的极限计算。
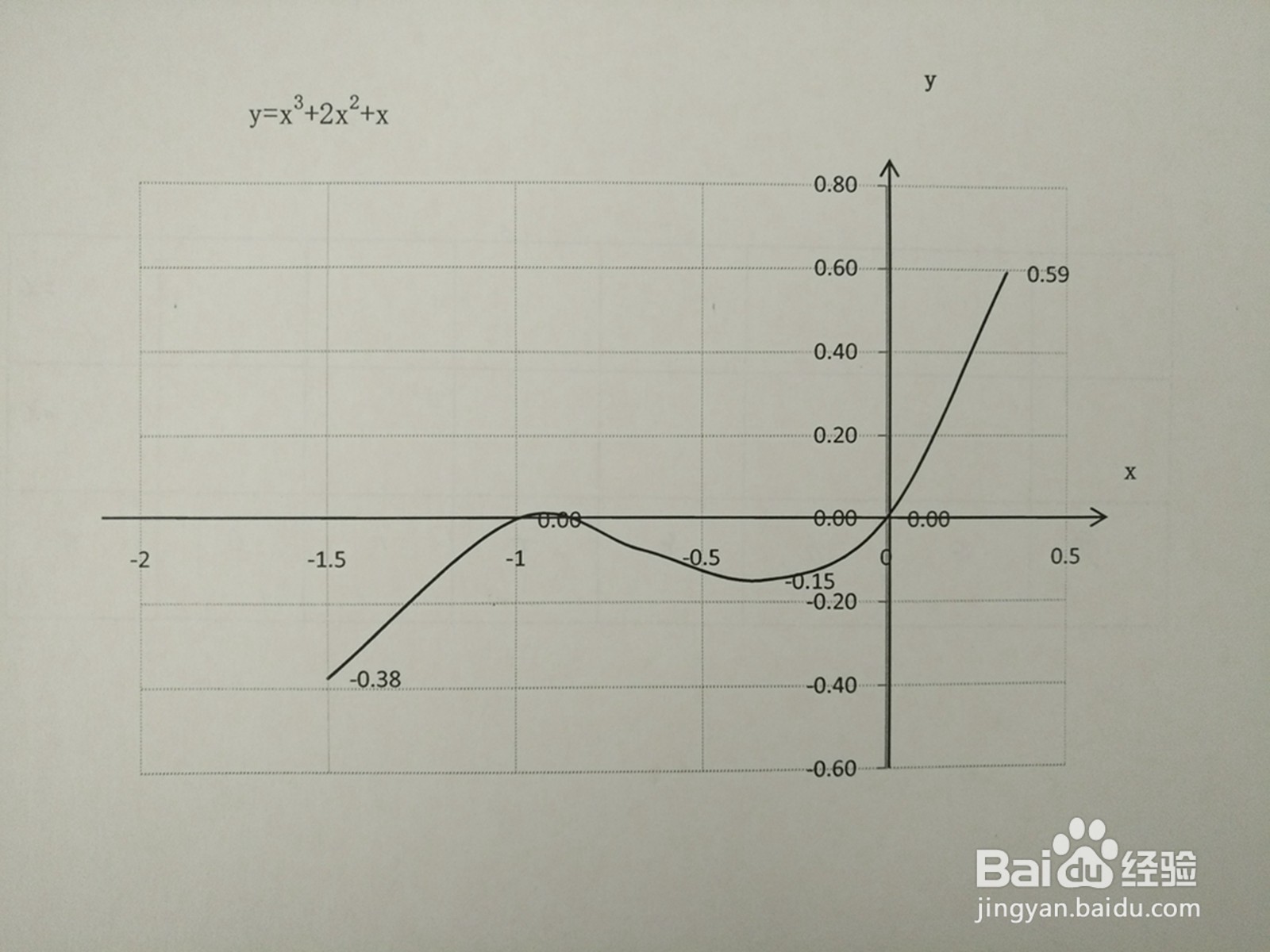
6、结合函数y=x^3+2x^2+x的定义域等性质,列举函数y=x^3+2x^2+x上的部分点构成的五点图。
7、根据函数的定义域,同时结合函数的单调性、凸凹性和极限等函数性质,通过五点图,在直角坐标系上即可画出函数y=x^3+2x^2+x的示意图如下。