怎么用FindArgMax来寻俣挫呲蹀找函数在什么地方取得局部最大值？本文首先介绍一下，用常规的求导数零点的方法来计算极大值，然后对比一下FindArgMax的好处和弊端。
工具/原料
电脑
Mathematica
一元函数
1、给定一元函数：x^3 + 6*x^2 + 2*x - 1图像如下，注意坐标刻度不一致。
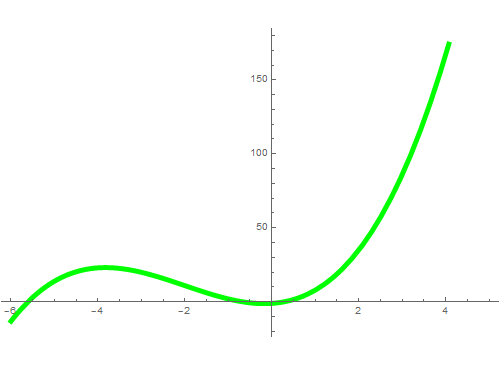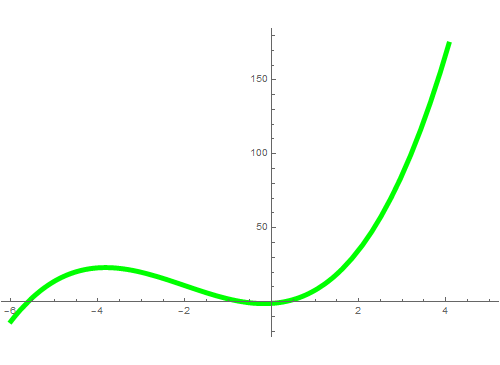
2、计算导函数的零点，再对比上图，可以发现，这个函数在(-6 - Sqrt[30])/3有极大值。
3、计算极大值：(99 + 20 Sqrt[30])/9。
4、尝试着用FindArgMax来搜索极值点的位置，先在-2附近寻找，结果还真找到了。
5、但是，如果从-0.1出发，就难以寻到极大值的位置：FindArgMax: 无法在 100 次迭代中收敛到要求的准确度或者精度.
6、这是因为-0.1已经是位于导函数的另一个单调区间了，或者说与极大值点分开在两个不同的单调区间里面。为了验证一下，分别尝试-0.17和-0.18，结论很明显。
二元函数
1、Sin[x + 3 y] - Cos[3*x - y]的图像。
2、求偏导数的零点。
3、先试着在{0.1,0.5}附近寻找极大值点。但是这个极值点跑到图形外面去了。
4、扩大绘图区域，把上一步的极大值点画在曲面上。可以发现，这确实是一个极大值点。
5、但是在{0.2,0.5}附近，基本上不能找到极大值点的位置。
