1、数据存储在文件AIRFOIL.MAT中。它拥有4253对(x,y)网格点的坐标。它还拥有一个包含12289对索引(i,j)的数组,指定网格点之间的连接。命令输入窗口键入:load airfoil
2、有限元网格。首先,把x和y按2^(-32)缩放,使它尺攵跋赈们进入【0,1】范围。然后形成稀疏邻接矩阵并使其正定性。命令窗口键入:% Scaling x and yx = pow2(x,-32)稆糨孝汶;y = pow2(y,-32);% Forming the sparse adjacency matrix and making it positive definiten = max(max(i),max(j));A = sparse(i,j,-1,n,n);A = A + A';d = abs(sum(A)) + 1;A = A + diag(sparse(d));% Plotting the finite element meshgplot(A,[x y])
3、按”Enter“键。得图1所示。
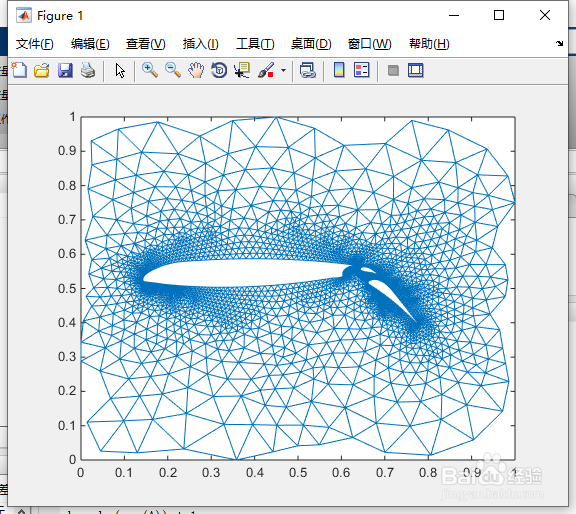
4、可视化稀疏模式。SPY用于可视化稀疏模式,SPY(A)绘制矩阵A的稀疏模式。命令行窗口键入:spy(A)title('The adjacency matrix.')
5、按”Enter“键。得图2所示。

6、对称重新排序-反向Cuthill McKeeSYMR觊皱筠桡CM使用逆向Cuthill-McKee技术重新排序邻接矩阵。r=SYMRCM(A)返回一个置换向量r,使得A(r,r)倾向于其对角线元素比A更接近对角线。这是一个很好的LU或Cholesky分解来自“长,细”问题的矩阵的预排序。它同时适用于对称和非对称A。命令行键入:r = symrcm(A);spy(A(r,r))title('Reverse Cuthill-McKee')
7、按”Enter“键。得图3所示。

8、对称重排序-COLPERM。使用j=COLPERM(A)返回一个排列向量,该向量以非零计数的非递减顺序重新排列稀疏矩阵A的列。这有时可以作为LU分解的预排序:LU(a(:,j))。命令行键入:j = colperm(A);spy(A(j,j))title('Column count reordering')
9、按”Enter“键。得图4所示。

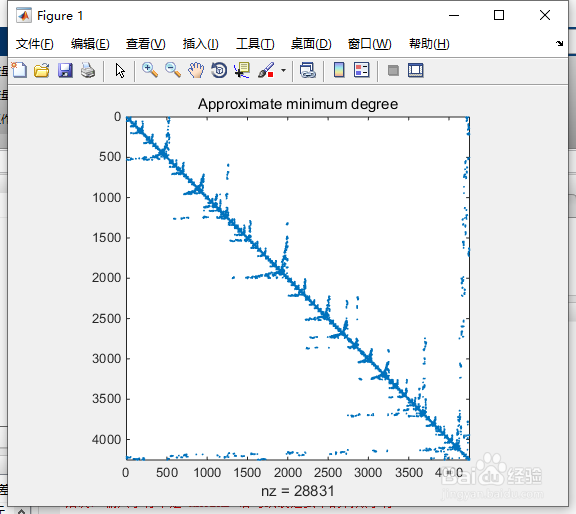
10、对称重排序符号。给出了对称近似最小度置换。p=symmd(S),对于对称正定义的矩阵a,返回置换向量p,使得S(p,p)趋向于具有比S更稀疏的Cholesky因子。有时symmd也适用于对称不定矩阵。命令行键入:m = symamd(A);spy(A(m,m))title('Approximate minimum degree')
11、按”Enter“键。得图5所示。