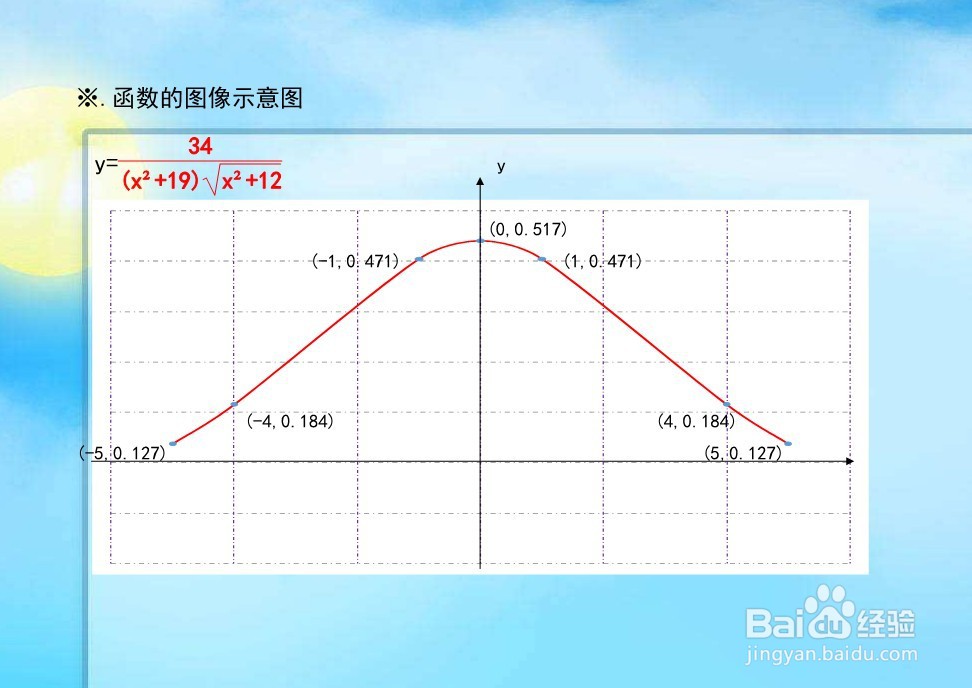
1、 解析函数的定义域,因为分母为两项的乘积,各项均为非零实数,故函数的自变量x可以取任意实数,即函数的定义域为:(-∞,+∞)。

2、函数的定义域可以是任何集合,腻戴怯猡包括实数集、复数集、有理数集等。然而,在实际应用中,我们通常需要根据具体问题来确定函数的定义域。例如,在物理学中,我们常常需要研究各种物理量之间的关系,这时就需要根据实际情况来确定函数的定义域。又如,在经济学中,我们常常需要研究各种经济因素之间的相互作用,这时也需要根据实际情况来确定函数的定义域。
3、本题介绍通过导数的知识,计算函数的一阶导数,即可得到函数的驻点,根据驻点判断一阶导数的符号,来解析函数的单调性并求出函数的单调区间。

4、解析函数的奇偶性质,可知函数为偶函数,并计算函数无穷远处的极限计算。

5、解析函数的五点图,综合函数定义域、奇偶性质等特殊点,函数上部分点解析表如下:
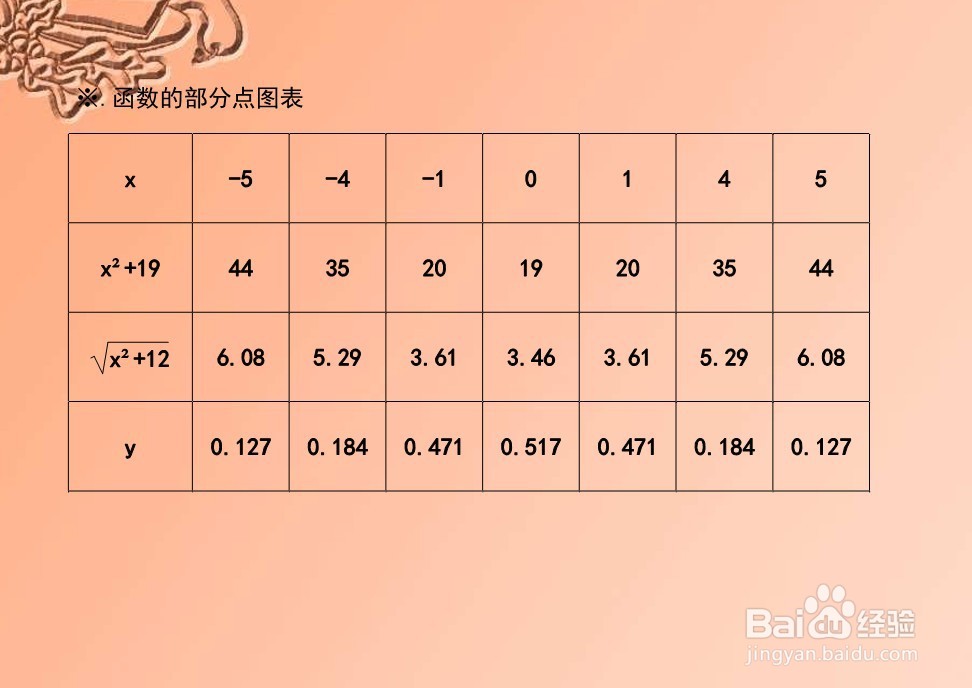
6、综合以上函数的相关性质,结合函数的定义域,即可简要画出函数的示意图如下图所示。