1、函数的定义域是指所有合法的输入值的集合。函数的定义域可以是任何集合,但通常是实数集或整数集等。

2、 求出函数的一阶导数,解析函数的单调性,即可知在定义域范围函数为单调减函数。

3、函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。
4、计算出函数的二阶导数,根据函数的二阶导数的符号,判断函数的凸凹性,并解析函数的凸凹区间。

5、计算该对数函数在无穷处和间断点处的极限。

6、根据定义域,结合函数的单调性和凸凹性,则函数图上,部分点以图表解析表列举如下:
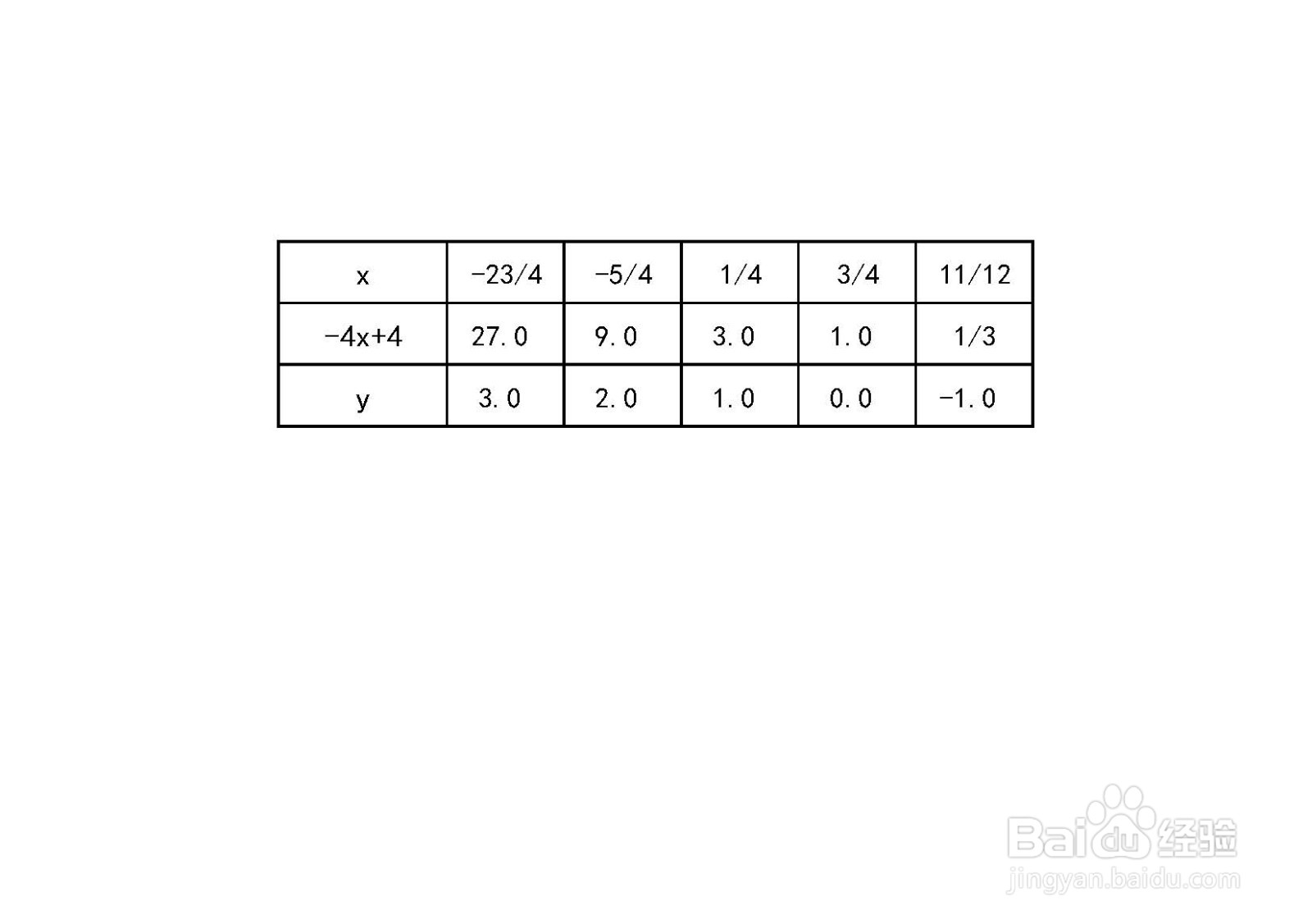
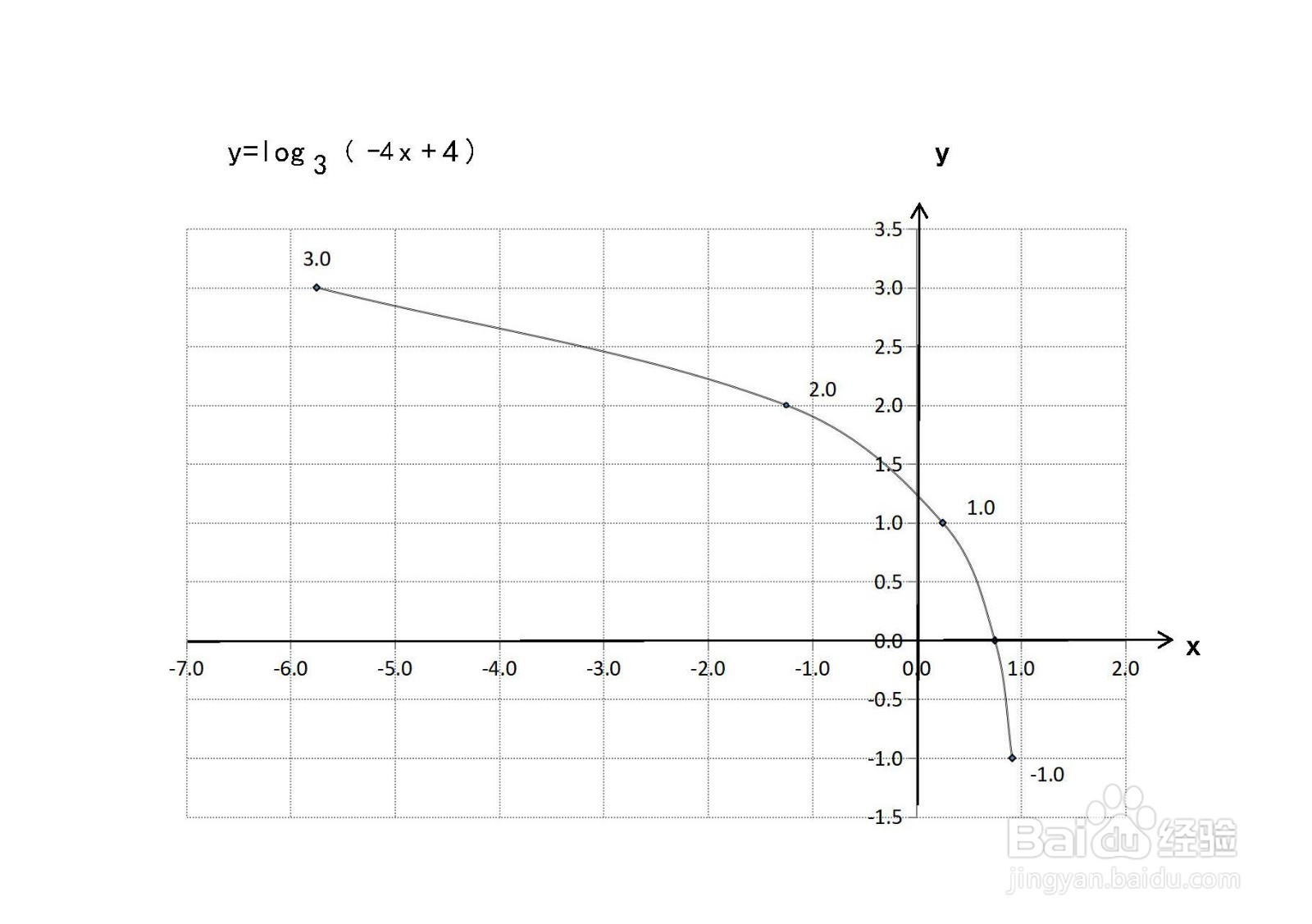
7、综合以上性质,函数的示意图如下: