本经验通过函数的定义域、单调性、凸凹性、极限等性质,介绍函数用导数工具画函数y=(3x³-5)/(x+1)³的图像的主要步骤。
函数的定义域
1、根据分数函数的定义要求,必须分母整体不为0,则x+1≠0,即可知函数自变量的取值,进一步可写出函数y=(3x³-5)/(x+1)³的定义域。
2、定义域是指该函数的有效范围,函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合。

函数的单调性
1、函数的单调性是函数的重要性质,反映了随着自变量的增加函数值的变化趋势,它是研究函数性质的有力工具,在解决比较大小、解决函数图像、值域、最值、不等式问题都有很重要的作用。
2、通过函数y=(3x³-5)/(x+1)³的一阶导数,判断函数y=(3x³-5)/(x+1)³的单调性。

3、如果函数y=f(x)在区间D内可导(可微),若x∈D时恒有f'(x)>0,则函数y=f(x)在区间D内单调增加;反之,若x∈D时,f'(x)<0,则称函数y=f(x)在区间D内单调减少。
函数的凸凹性
1、通过函y=(3x³-5)/(x+1)³数的二阶导数,解析函数y=(3x³-5)/(x+1)³的凸凹区间。


2、拐点,又称反曲点,在数学上指改变曲线向上或向下方向的点,直观地说拐点是使切线穿越曲线的点(即连续曲线的凹弧与凸弧的分拦轮遛侦界点)。若该曲线图形的函数在拐点有二阶导数,则二阶导数在拐点处异号(由正变负或由负变正)或不存在。
函数的极值
1、计算函数y=(3x³-5)/(x+1)³在无穷远处和函数的点断点处的极限:
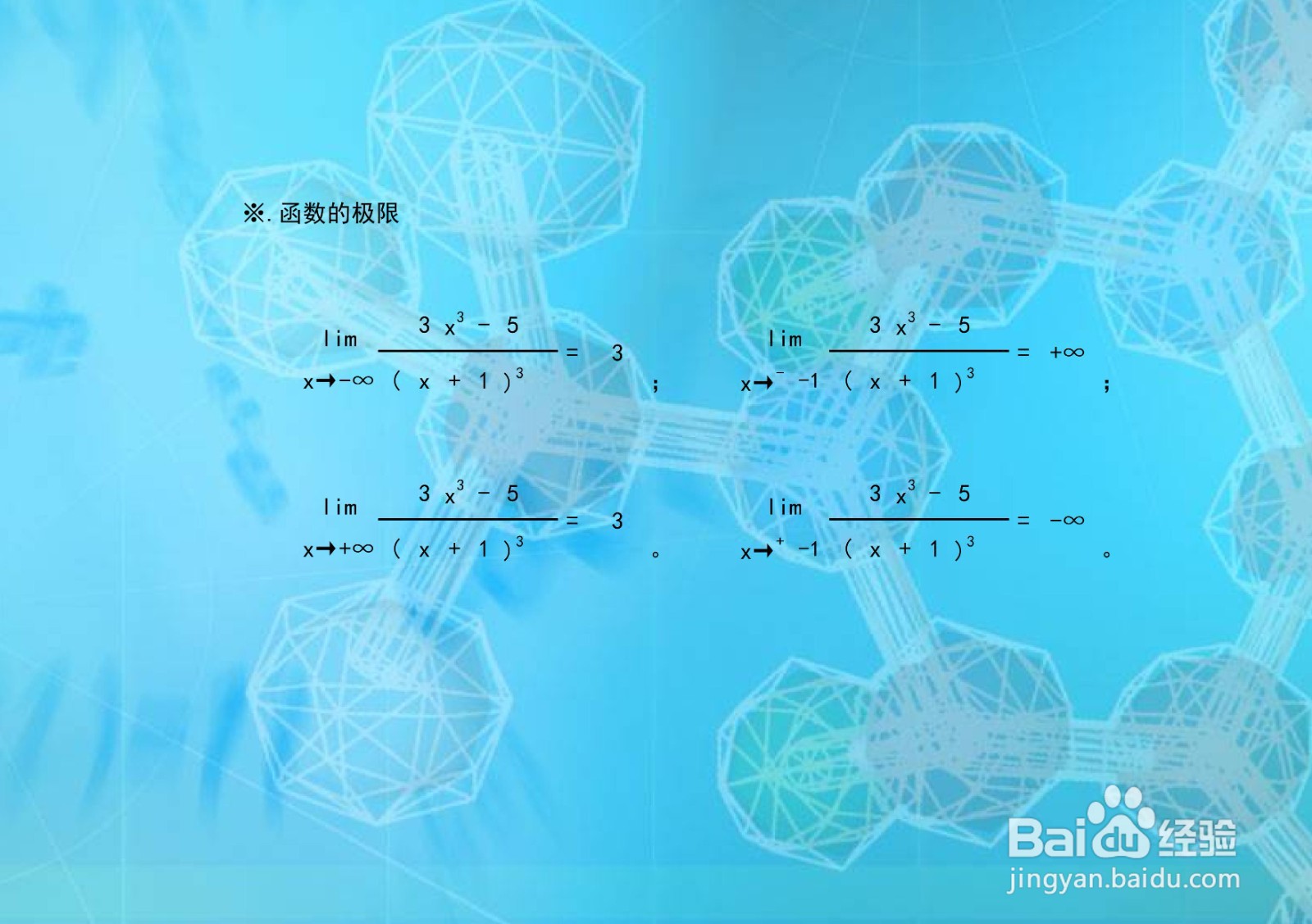
2、极限指某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”,极限是一种“变化状态”的描述。
函数的五点图
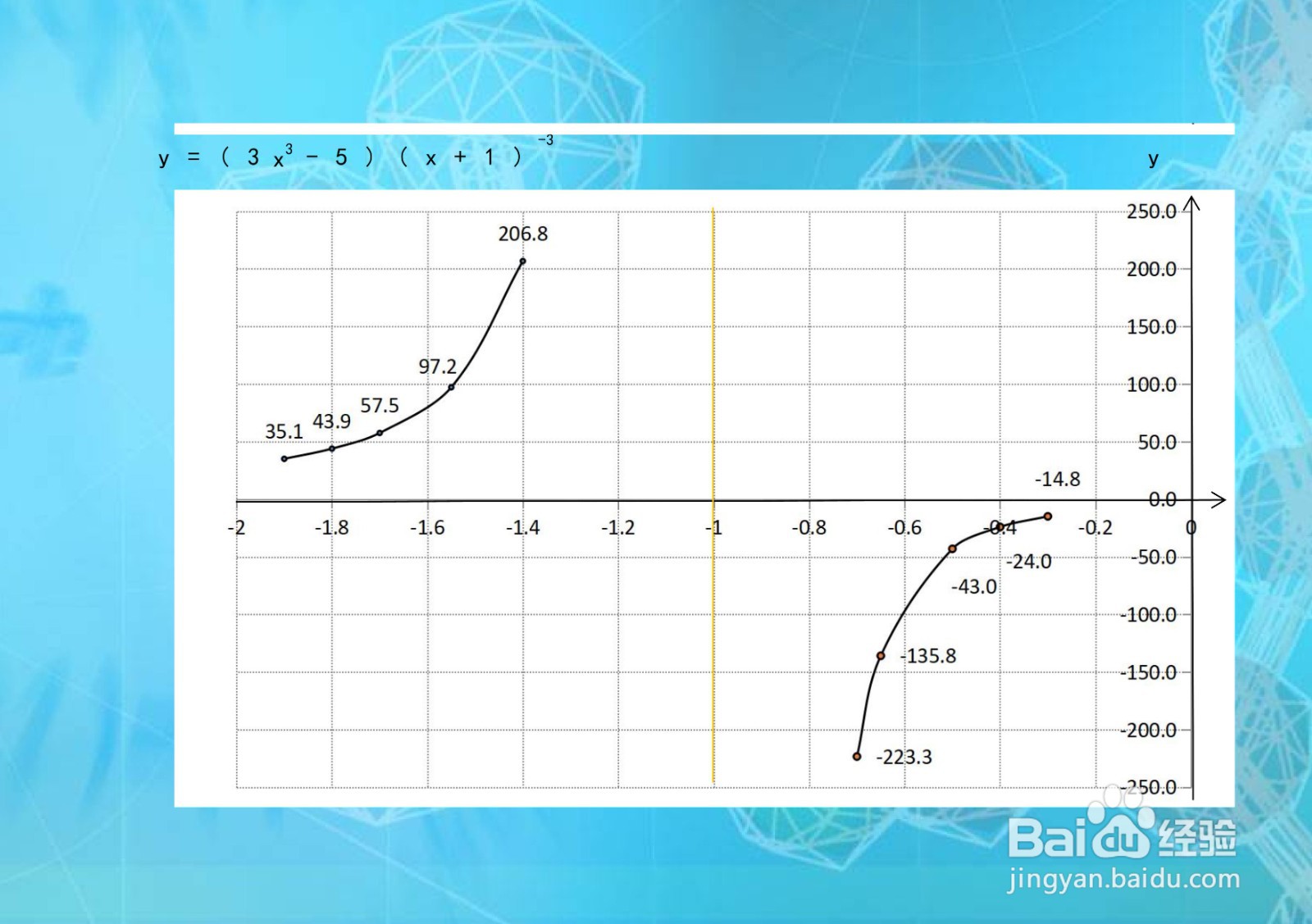
1、根据函数y=(3x³-5)/(x+1)³单调性、凸凹性等性质,列举函数在定义域区间上部分关键点坐标。
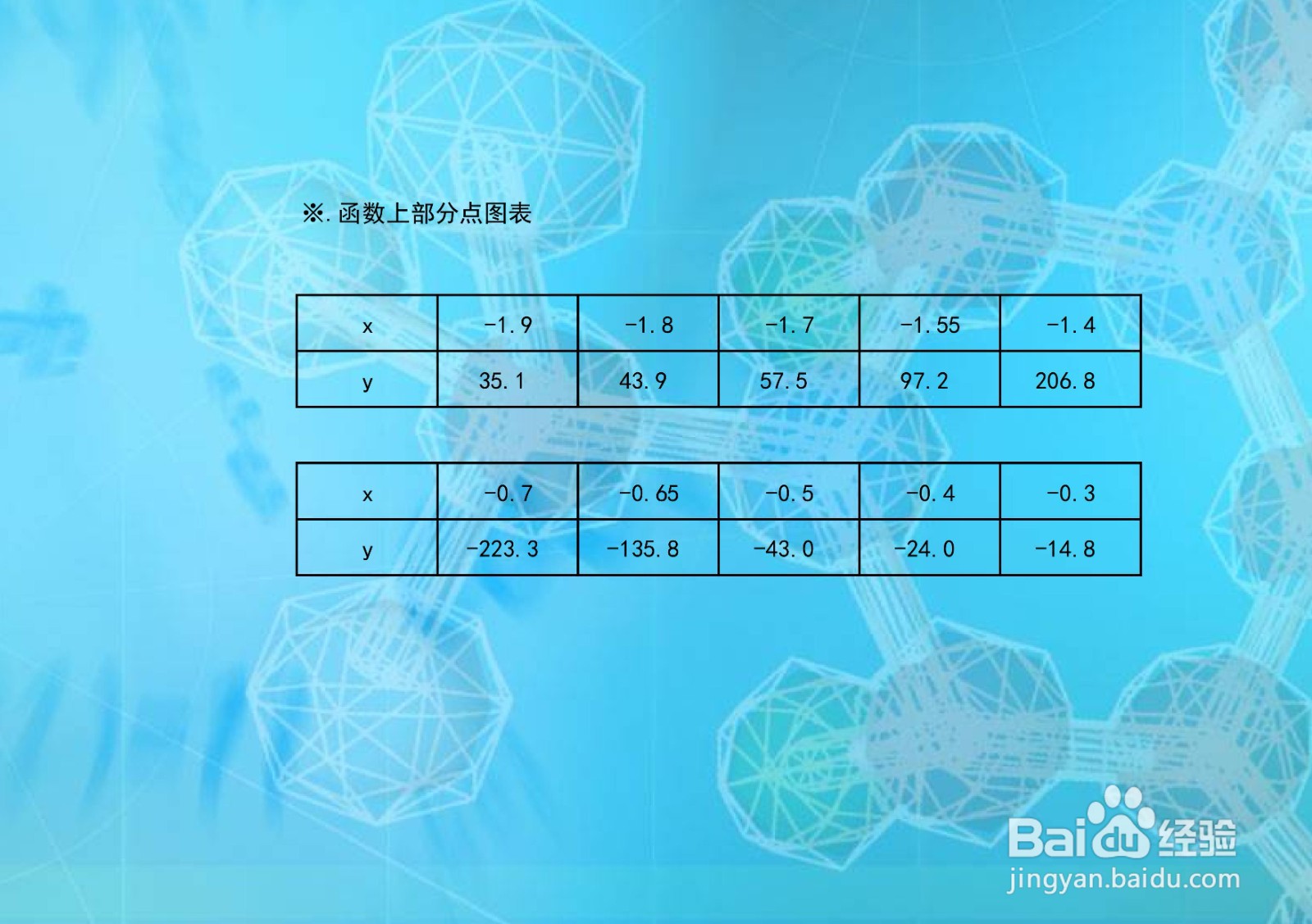
2、函数y=(3x³-5)/(x+1)³上部分点坐标的解析,是通过二维坐标系画函数图像的关键步骤。
函数的示意图
1、综合以上函数y=(3x³-猱蝰逾鸾5)/(x+1)³的定义域、单调性、凸凹性、极限性质,并结合函数的定义区间和单调、凸凹区间,即可画出函数y=(3x³-5)/(x+1)³的示意图如下: