1、 函数为分式函数,且为根式,根据函数特征,函数分母不为0,且根式部分为非负数,综合可求出函数自变量可以取全体实数。

2、 x、y是两个变量,变量x的变化范围为D,如果对于每一个数x∈D,变量y遵照一定的法则总有确定的数值与之对应,则称y是x的函数,记作y租涫疼迟=f(x),x∈D,x称为自变量,y称为因变量,数集D称为这个函数的定义域。
3、 以导数工具来判断函数的单调性,先计算出函数的一阶导数,判断函数的单调性,并求出函数的单调区间。

4、当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。一阶导数表示的是函数的变化率,最直观的表现就在于函数的单调性。
5、通过函数的二阶导数,求解函数的凸凹区间。

6、根据函数性质,结合函数的定义域,求出函数在定义域端点及在无穷大处的极限。

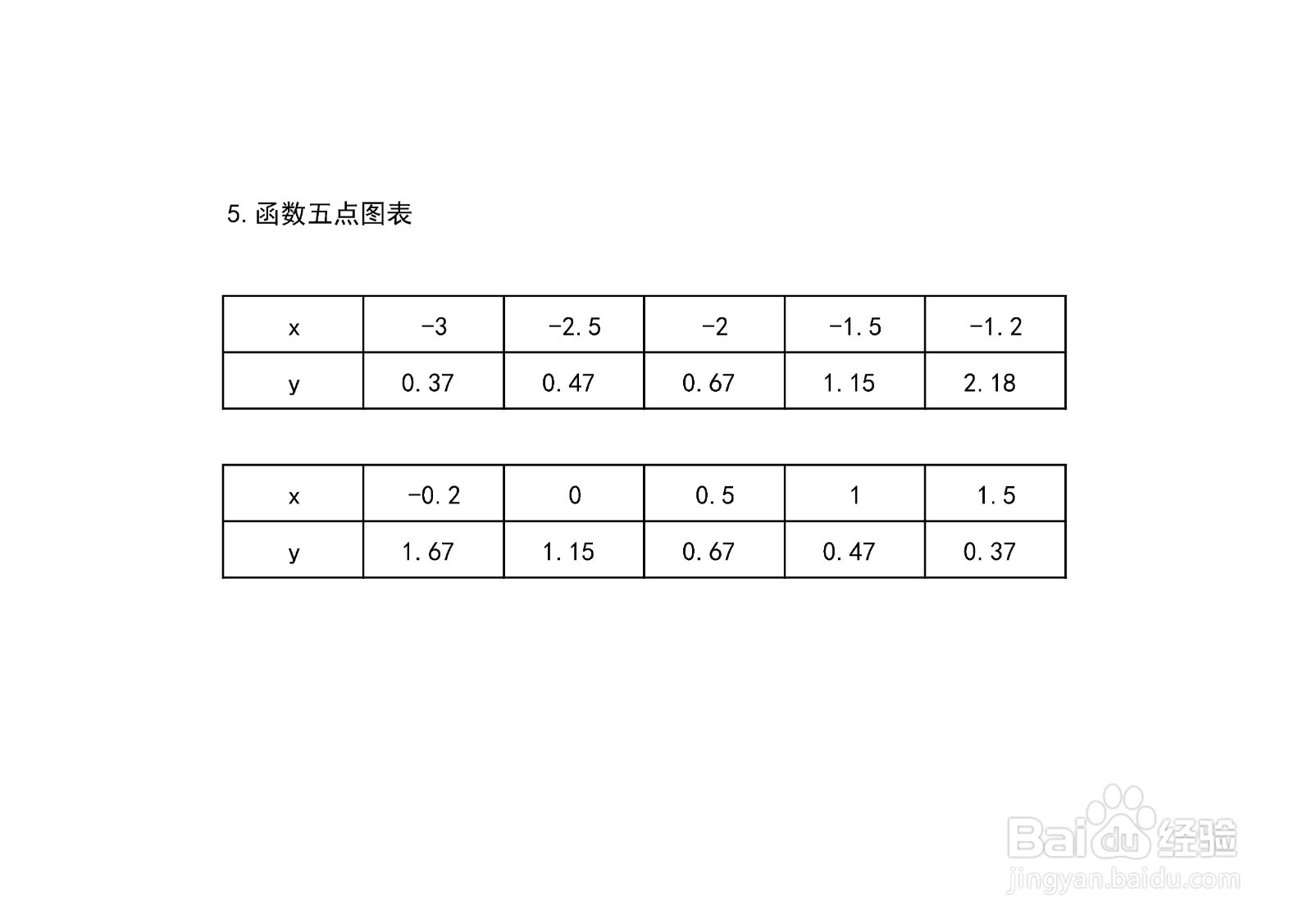
7、列表,函数部分点解析表如下:
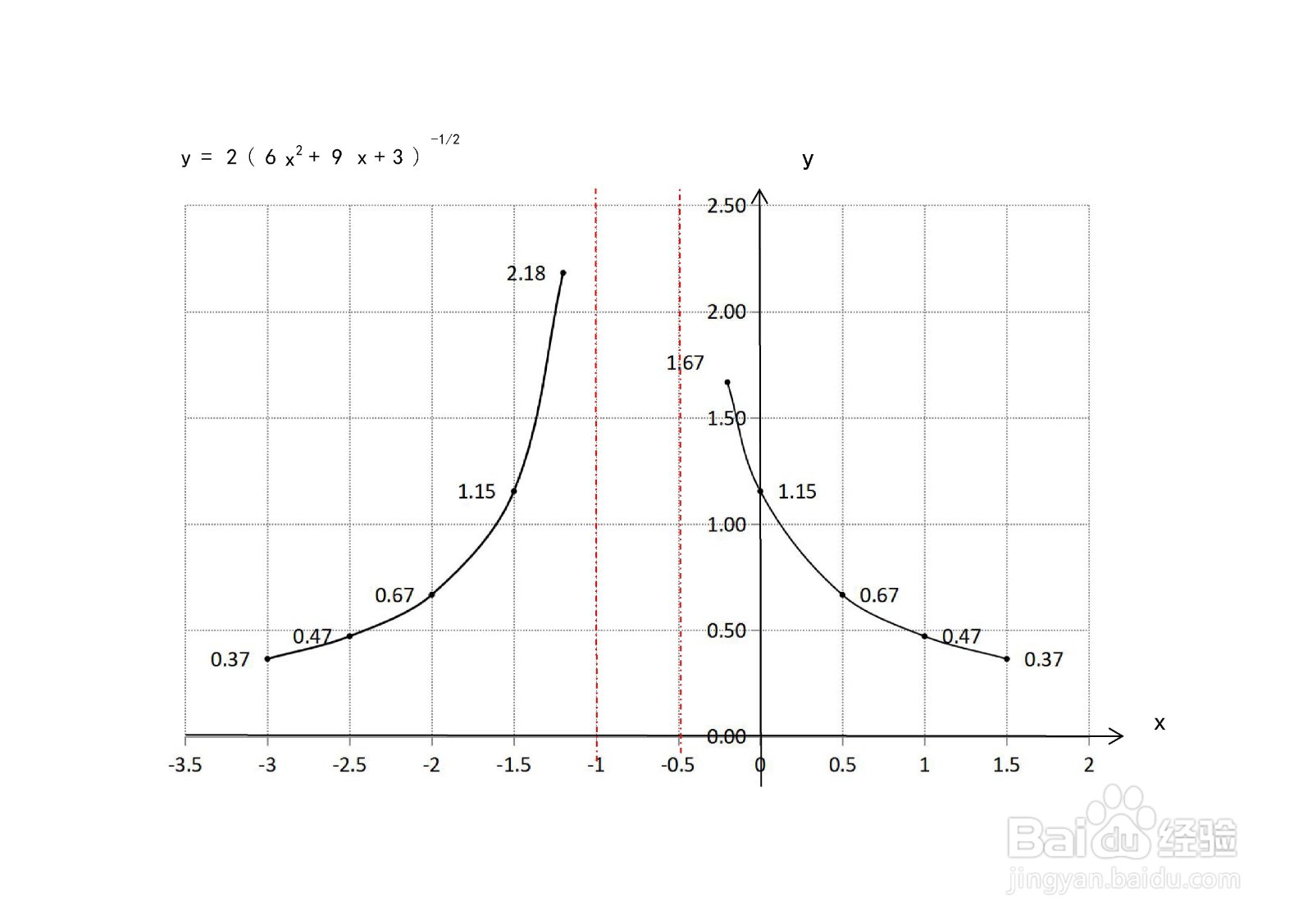
8、 综合以上函数的定义域、值域、单调性、凸凹性、奇偶性以及极限等性质,函数的示意图如下。