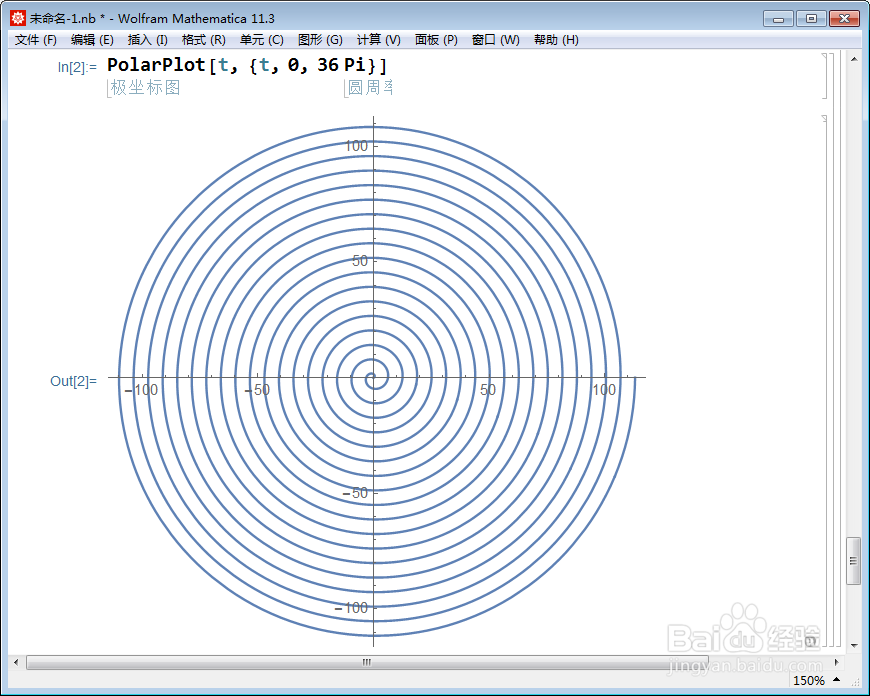
1、绘制螺旋线:
PolarPlot[t, {t, 0, 36 Pi}]
2、绘制球面:
Show[ParametricPlot3D[{Sin[u] Sin[v], Sin[u] Cos[v], Cos[u]}, {u, 0, 2 Pi}, {v, 0, Pi}]]
其中u和v是球面的曲纹坐标。

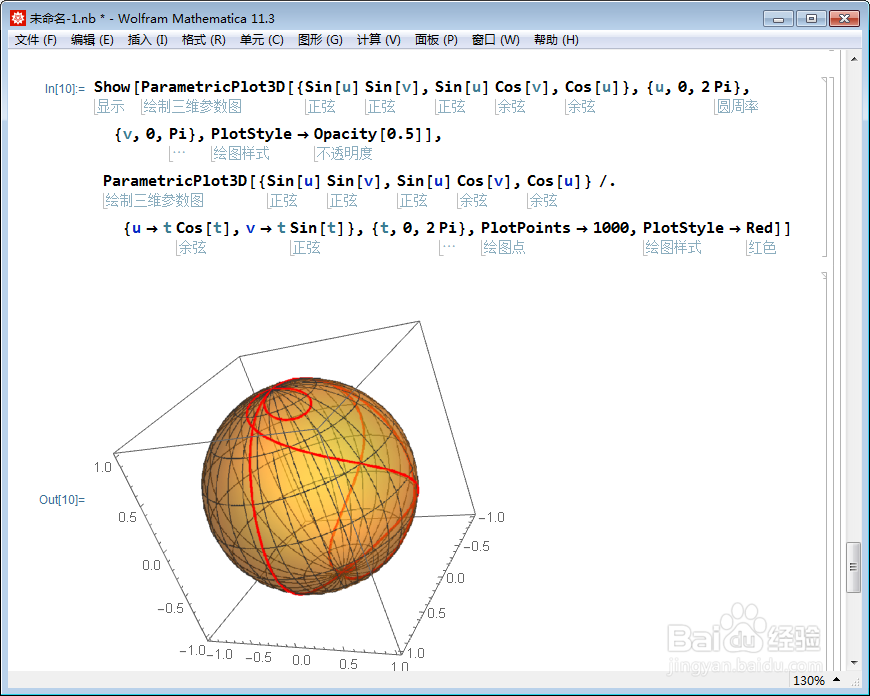
3、在球面上绘制螺旋线,需要把u和v变成关于t的函数式:
Show[ParametricPlot3D[{Sin[u] Sin[v], Sin[u] Cos[v], Cos[u]}, {u, 0,
2 Pi}, {v, 0, Pi}, PlotStyle -> Opacity[0.5]],
ParametricPlot3D[{Sin[u] Sin[v], Sin[u] Cos[v],
Cos[u]} /. {u -> t Cos[t], v -> t Sin[t]}, {t, 0, 2 Pi},
PlotPoints -> 1000, PlotStyle ->销鬼关 Red]]
4、缩:
ParametricPlot3D[{Sin[u] Sin[v], Sin[u] Cos[v],
Cos[u]} /. {u -> t/36 Cos[t], v -> t/36 Sin[t]}, {t, 0, 10 Pi},
PlotPoints -> 1000, PlotStyle -> Red]
效果如级怕下啊!

5、增量:
ParametricPlot3D[{Sin[u] Sin[v], Sin[u] Cos[v],
Cos[u]} /. {u -> t/36 Cos[t], v -> t/36 Sin[t]}, {t, 0, 36 Pi},
PlotPoints -> 1000, PlotStyle -> Red]
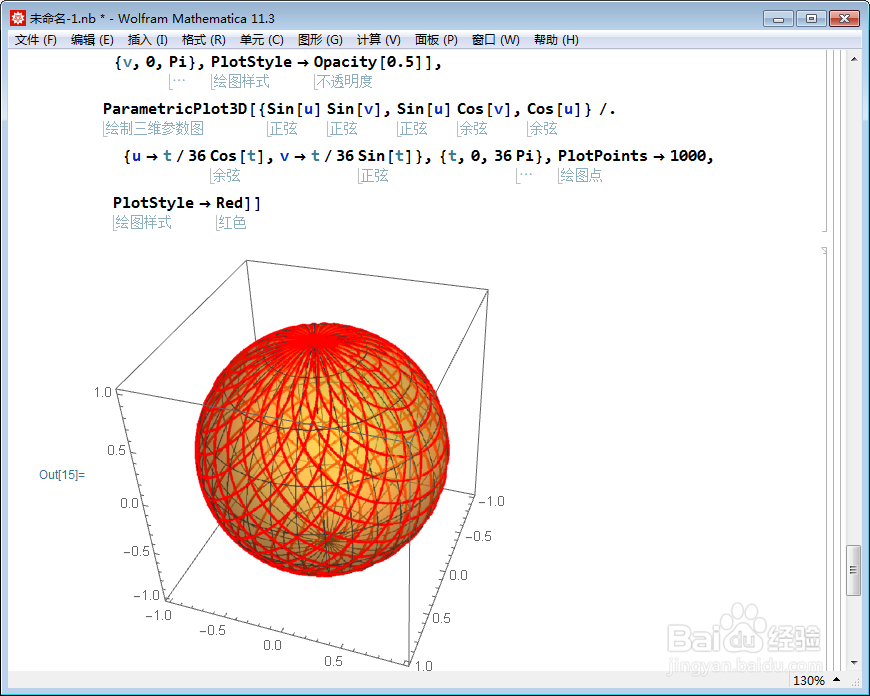
6、全方位观获率察这个球面螺旋。
