1、连接连心线AB,作半径BF⊥AB。

2、作△ABF的外接圆。
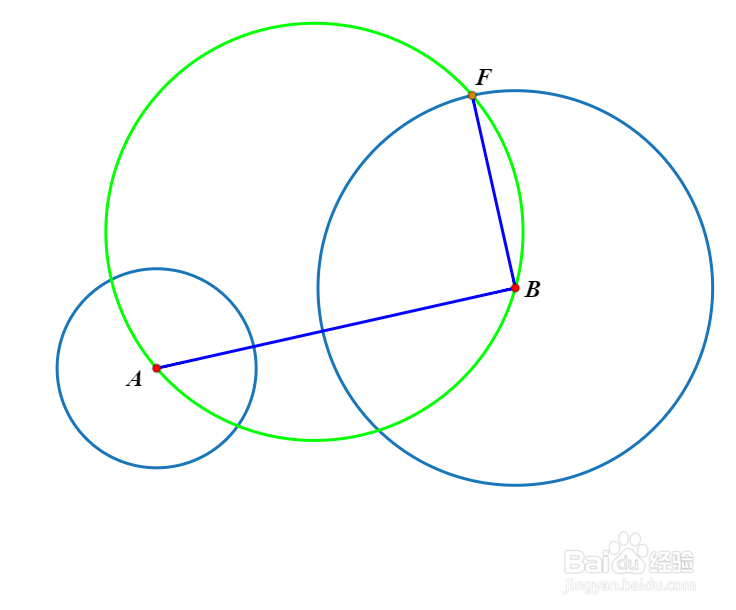
3、设圆ABF与圆A交于C、D两点。
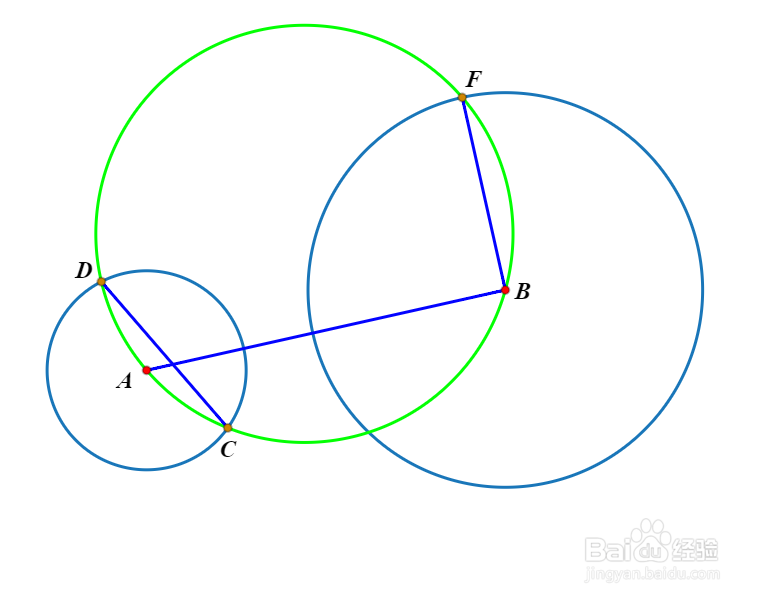
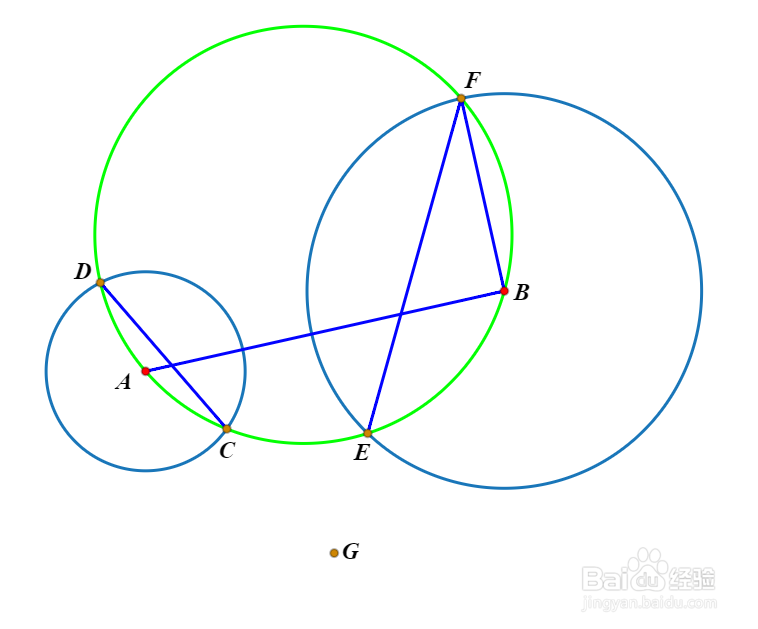
4、设圆ABF与圆B交于E、F两点(F点之前已经作出)。

5、CD和EF交于点G。.容易证明,G是圆A和圆B的一个等幂点。
6、G到AB的垂线,就是圆A和圆B的根轴。
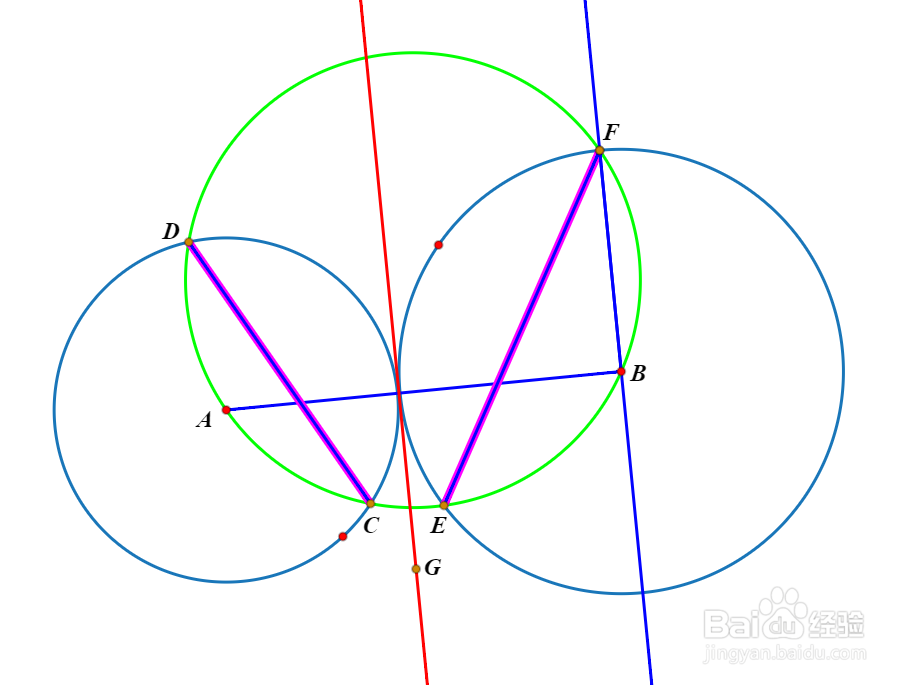
7、注意,只要圆A和圆B的半径不等于0且A、B不重合,那么CD和EF就不会平行,也就是说点G不会位于无限远的地方,这导致这个作图适用于不同心的两个圆的根轴作图。
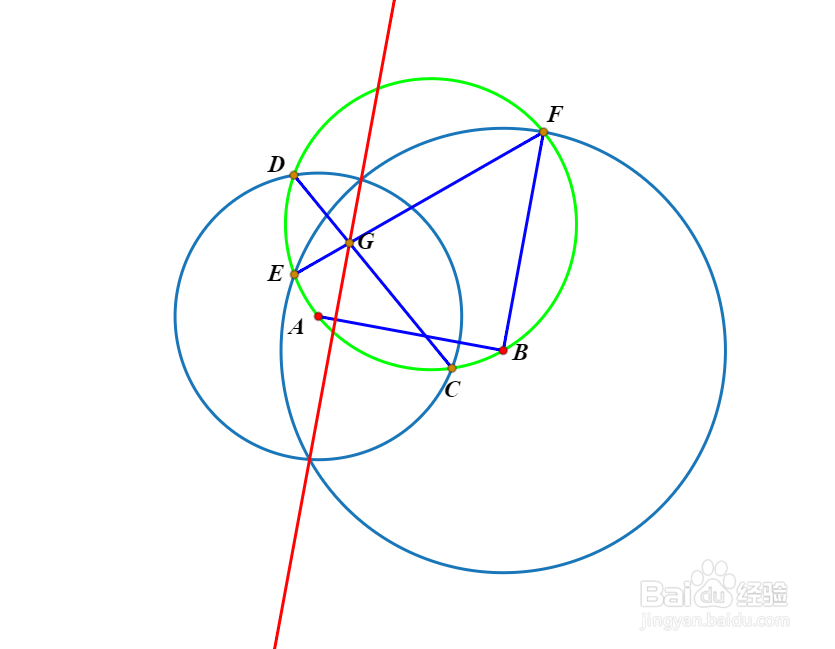
1、连接连心线AB,作半径BF⊥AB。

2、作△ABF的外接圆。

3、设圆ABF与圆A交于C、D两点。

4、设圆ABF与圆B交于E、F两点(F点之前已经作出)。

5、CD和EF交于点G。.容易证明,G是圆A和圆B的一个等幂点。

6、G到AB的垂线,就是圆A和圆B的根轴。

7、注意,只要圆A和圆B的半径不等于0且A、B不重合,那么CD和EF就不会平行,也就是说点G不会位于无限远的地方,这导致这个作图适用于不同心的两个圆的根轴作图。
