1、一阶微分方程的通式可表达为y’=f(x,y),可以通过观察是否可以分离变量来求出通解。

2、由y’=dy/dx可以把x、y的微分和自变量相互分离。
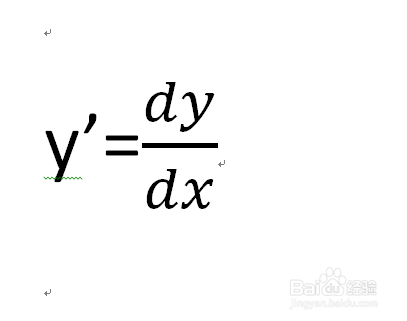
3、通过观察将其化为g(y)dy=f(x)dx的形式。
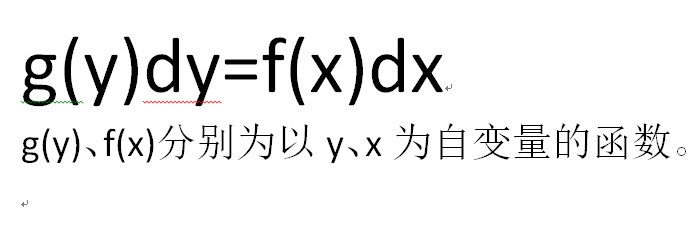
4、变量分离至等式两端时,两边同时积分。

5、应用积分知识,得出通解G(y)=F(x)+C。

1、一阶微分方程的通式可表达为y’=f(x,y),可以通过观察是否可以分离变量来求出通解。

2、由y’=dy/dx可以把x、y的微分和自变量相互分离。
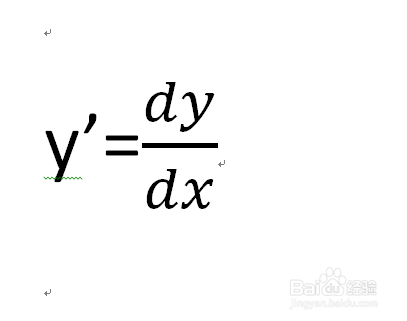
3、通过观察将其化为g(y)dy=f(x)dx的形式。
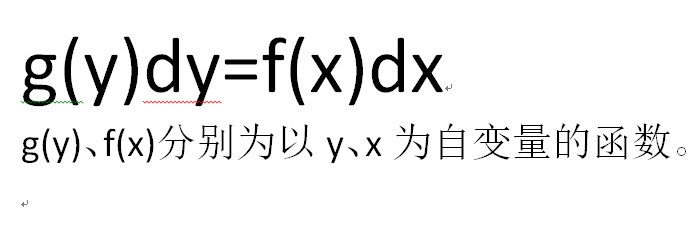
4、变量分离至等式两端时,两边同时积分。

5、应用积分知识,得出通解G(y)=F(x)+C。
