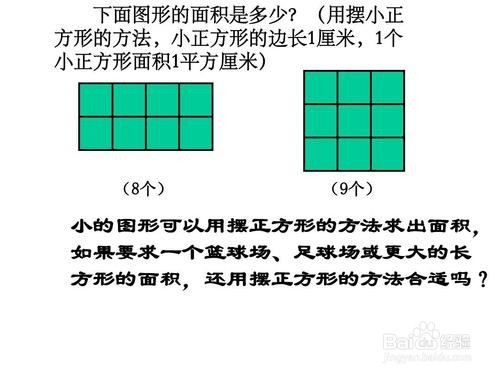
1、长方形面积公式的推导是高中平面几何的一个大课题。长宽都是整数:则用分块“数”数 ,即有S=MN.﹙M×N个﹙1×1﹚的方块﹚
2、长宽都是有理数,此时长宽有“公度”d:也用分块“数”数。不过方块比﹙1×1﹚小。是﹙d×d﹚例如长=11/23,宽=2,则d硐移噔泔=1/23 长=11﹙1/23﹚。宽=46﹙1/23﹚面积=11×46﹙1/23﹚²=﹙11/23﹚×2

3、长宽出现无理数:这时得用极限方法重新建立面积的概念。
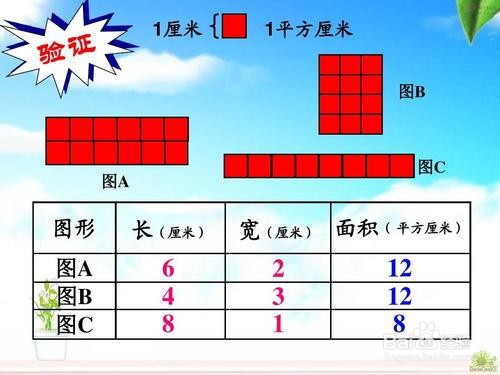
4、这其实也是微积分的思想,只要把它分解到无限小的单元就可以了。例如一平方米,把厘米看作不可”分割”,那么长就有100个厘米,宽就有100个,那么说”横”有100个”纵”也有一百个。全部加起来就是有一百个一百,就是说有一万平方厘米=一平方米。
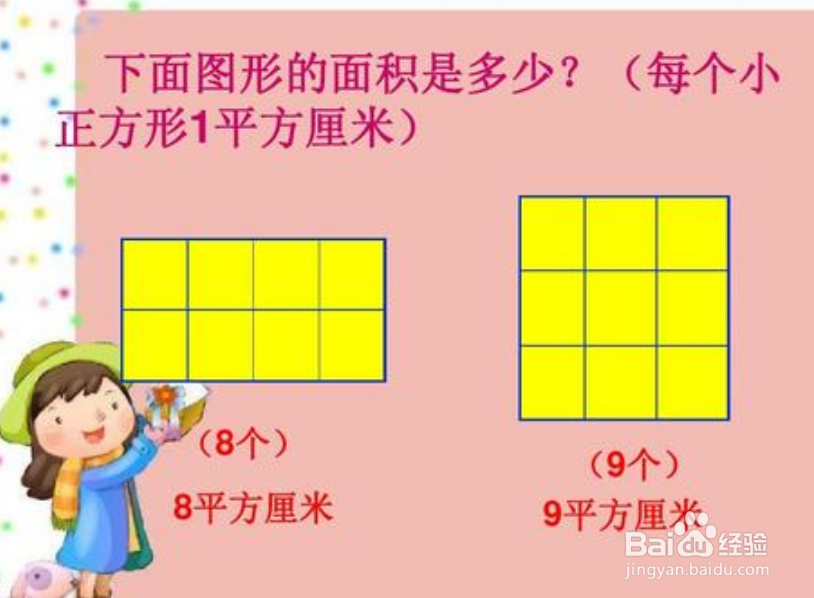
5、长方形是根据数格子推导出来的,正方形是根据长方形的面积公式得来的。

6、古人如何研究出长方形面积我不知道,但我知道有一种方法可以简单求出长方形面积公式,那就是直接在长方形上面画等面积格子,只要知道格子数量,就知道长方形的面积了,
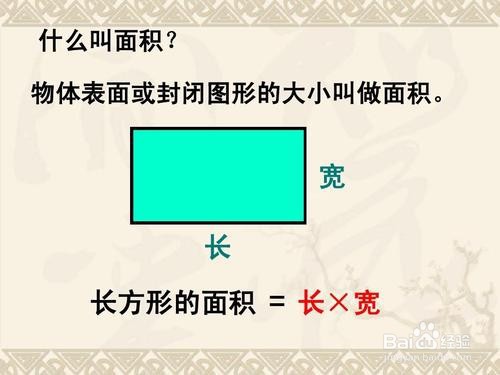
7、长方形的面积推导是在一个大长方形中一些面积为1平方厘米的小正方形,由小正方形的个数推出长方形的面积由长*宽得到。
