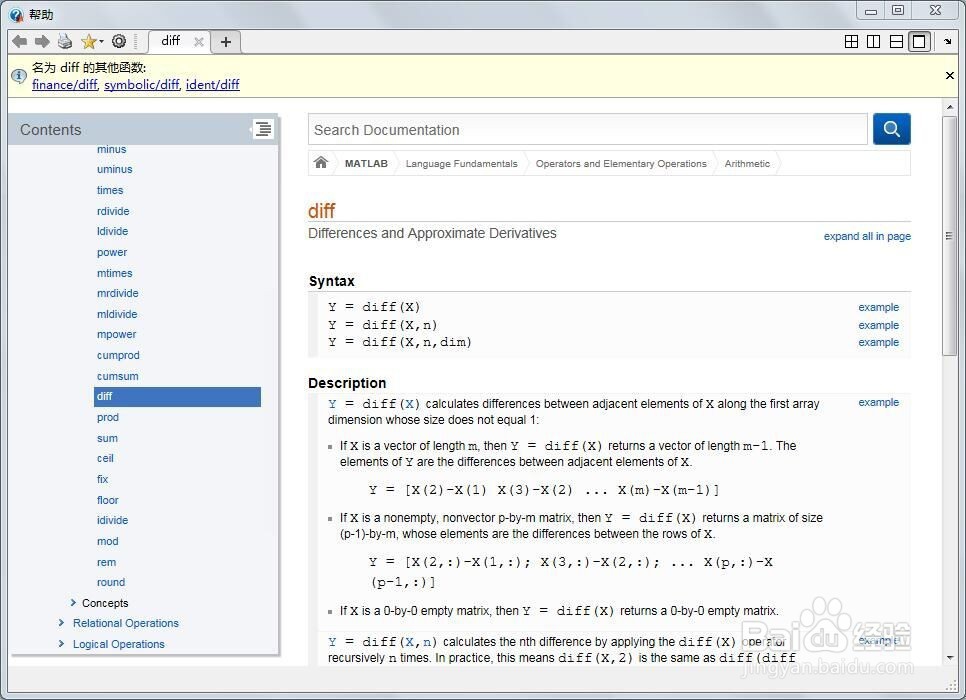
1、第一,首先给出这道考研数学真题,如下图,下面利用MATLAB解决这道题。

2、第二,给出函数的导数、拐点等概念。设函数y=f(x)在点x0的某个领域内有定义,自变量x在垓矗梅吒x0处的增量为∆x,相应的函数增量为∆y=f(x0+∆x像粜杵泳)-f(x0),如果∆y/∆x在∆x趋近于0时的极限存在,那么就称函数y=f(x)在点x0处可导,并称这个极限为函数y=f(x)在点x0处的导数,记作f'(x0)。函数y=f(x)在点x0处的一阶导数的几何意义表示曲线y=f(x)在点(x0,f(x0))处的斜率。一阶导数f'(x)关于自变量x再求导数得到二阶导数f''(x)。对于函数曲线而言,极值点处一阶导数为0,拐点处二阶导数为0;一阶导数刻画的是函数曲线的增减性,二阶导数刻画是函数曲线的凹凸性,拐点两侧二阶导数异号。形象地讲,拐点是曲线向下方向或者向上方向开始改变的点。

3、第三,启动MATLAB,输入如下代码,求解上述函数曲线的一阶导数、二阶导数、拐点和拐点处的吨易坌荐切线方程。close all; clear all; 艘早祓胂clc;format compact% MATLAB之考研数学:函数的导数和求函数在拐点处的切线方程syms x % 声明符号变量xassume(x > 0) % x的定义域大于0y = x^2+2*log(x); % 符号变量x表示的曲线函数yd1 = diff(y,x,1) % 求函数y的一阶导数d2 = diff(y,x,2) % 求函数y的二阶导数x0 = solve(d2,0) % 求二阶导数为0时的点(即拐点)y0 = subs(y,x,x0) % 拐点处的y值k = subs(d1,x0) % 拐点处的切线斜率f = k*(x-x0)+y0 % 拐点处的切线方程%---------绘制函数曲线和切线方程的图像----------%fplot(inline(y),[0.1,5],'r-');hold onfplot(inline(f),[0.1,5],'k-');hold offtext(double(x0),double(y0),'\leftarrow 拐点(1,1)')xlabel('\fontsize{15}X');ylabel('\fontsize{15}Y')legend('函数曲线 y=x^2+2ln(x)','切线方程 f=4x-3','Location','NorthWest')set(gca,'FontSize',13,'TickDir','out','TickLength',[0.02,0.02])axis fill

4、第四,保存和运行上述脚本,在命令行窗口得到函数曲线的一阶导数为2x+2/x、二阶导数为2-2/x^2,拐点为(1,1),拐点处的切线方程为y=4x-3,与正确答案一致。
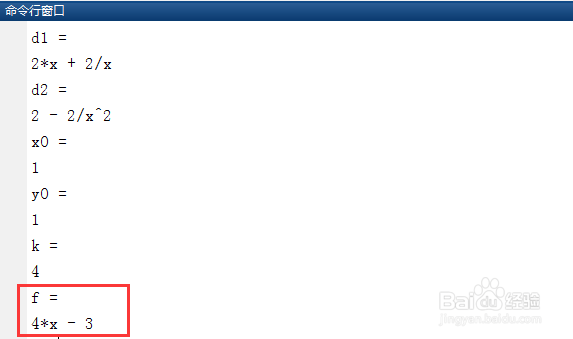
5、第五,同时得到函数的曲线、切线方程和拐点的图像如下图,拐点为(1,1)。

6、第六,第三步代码中,syms用于声明符号变量assume()用于设置符号变量的数学属性,比如本文assume(x>0)就是设置x为大于0的符号变量diff()用于求函数的导数,其常用的调用格式为diff(fx,x,n),其中fx为符号变量表示的函数,x为符号变量,n为求导的阶数,n=1表示求一阶导数,n=2表示求二阶导数。更多diff( )的用法请见MATLAB帮助文档。