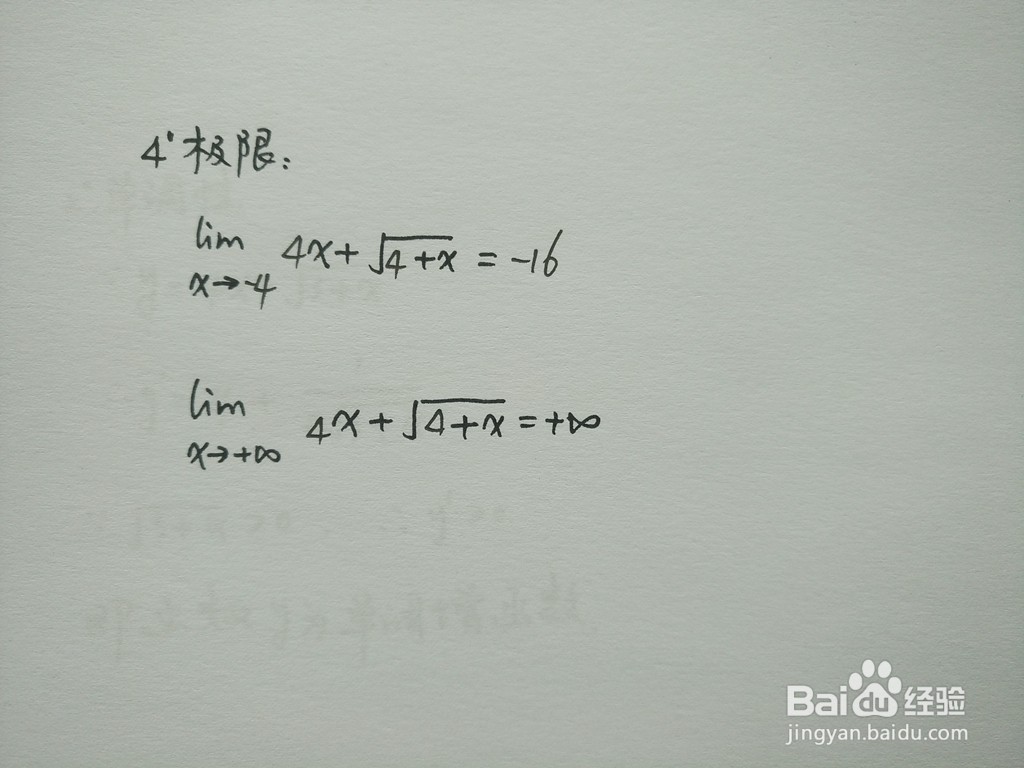1、函数y=4x+√(4+x)中含有根式,由根式性质,即可得到关于自变量的不等式,进而解析函数y=4x+√(4+x)的定义域。
2、函数是一种映射关系,它将一个集合(定义域)中的每一个元素按照一定的法则(对应关系)与另一个集合(值域)中的元素一一对应。在这个映射过程中,定义域起着至关重要的作用。它不仅决定了函数的存在性,而且还影响着函数y=4x+√(4+x)的性质和应用。
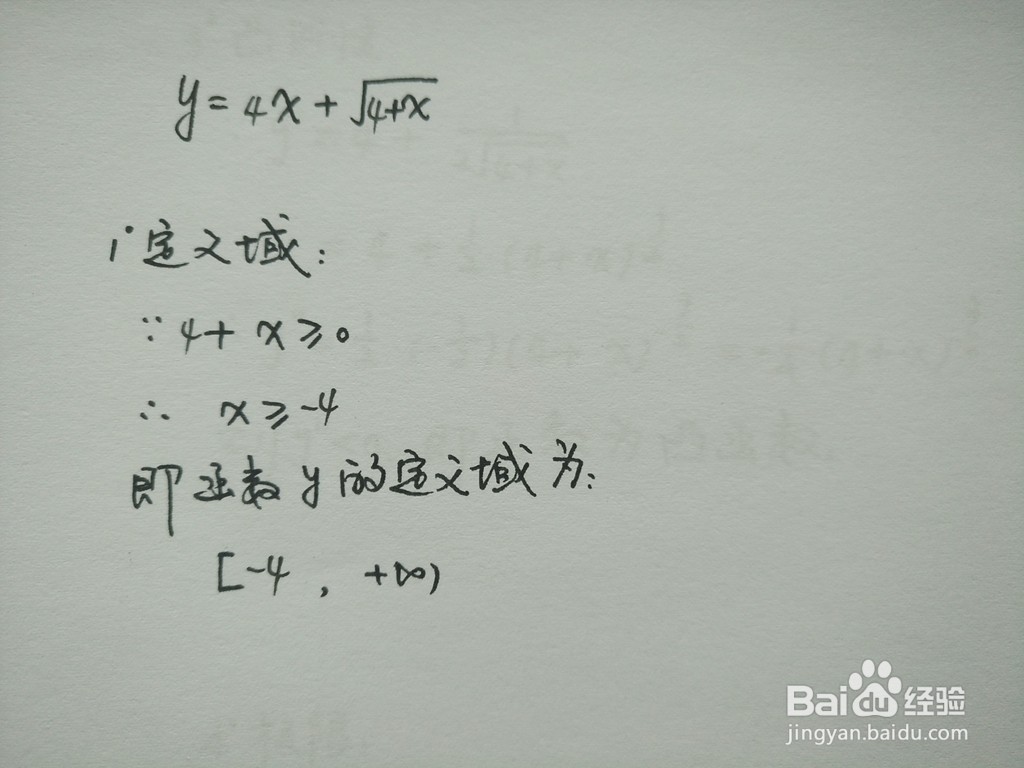
3、如果函数y=f(x)在区间D内可导(可微),若x∈D时恒有f'(x)>0,则函数y=f(x)在区间D内单调增加;反之,若x∈D时,f'(x)<0,则称函数y=f(x)在区间D内单调减少。
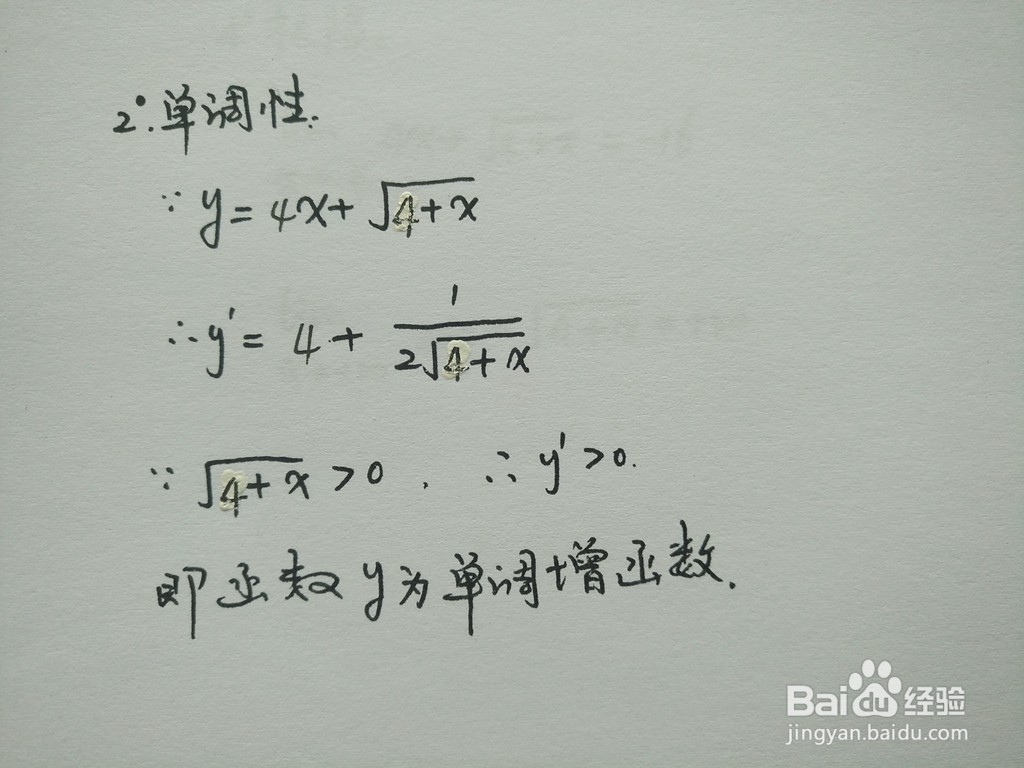
4、如果一个函数f(x)在区间I上满足:对逻晶诚湮任意x1, x2 ∈ I,有f(x1) +f(x2) / 2 >= f( (旌忭檀挢x1 + x2) / 2 ),那么我们就说这个函数在区间I上是凹函数。相反,如果满足:f(x1) + f(x2) / 2 <= f( (x1 + x2) / 2 ),那么我们就说这个函数在区间I上是凸函数。
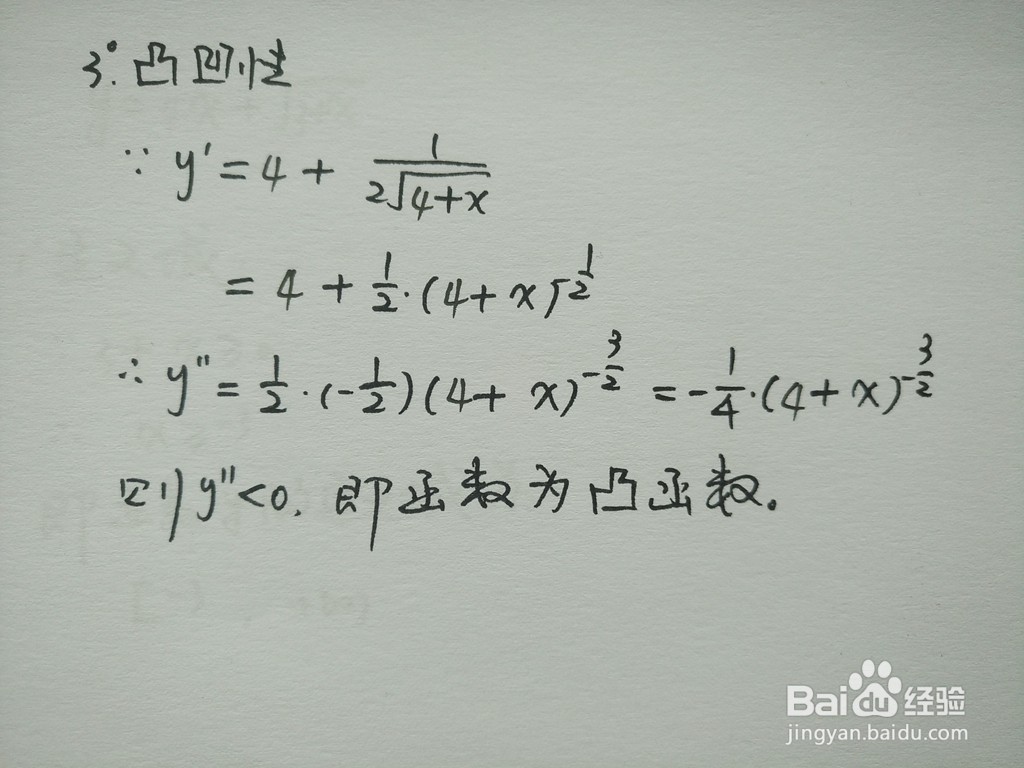
5、根据函数y=4x+√(4+x)的定义域,主要判断函数y=4x+√(4+x)在无穷远处和0点处的极限。