1、 我们在讲技巧之前还是先讲一些理论东西,同学们我想要说一下,向量四心问题快速求解的秘密--特殊化,那这个三角形特殊在什么地方呢?向量四心指的又是哪四心呢?我要告诉大家,有重心、垂心、外心和内心。
重心是什么线的交点,应该是中线的交点,我用G表达。垂心呢?三条高线的交点,外心呢?注意是中垂线交点,而内心呢?是角分线的交点。那么这四个心怎样记忆呢?我们在正课里面讲的非常清楚,同学们值得注意的是这四个心它有不同的向量表述,请看下图。
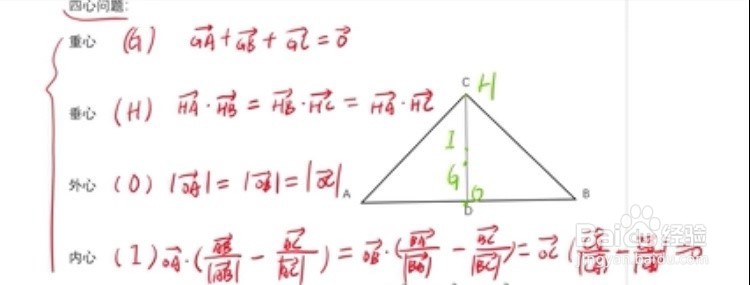
2、 用常规的方法看这种题目肯定在短时间内搞不定的,稍后给大家分享两道题,你就明白了。同学们,记住我们四心问题特殊化是特殊化成什么呢,其实这就是个等腰Rt三角形,这个很管用,不要特殊中等边,因为等边三角形四心合一,而等腰Rt三角形四心就不是一个心。但是四心有一个特征点,就是都在这个CD高线上,而我所给的这个三角形ABC就是一个等腰Rt三角形,注意图中,外心O与D点重合,重心G到三个顶点的距离相等,而内心I呢?到三条边的距离相等,垂心H自然就是C点了,与C点重合。
所以一般的三角形是不满足这种关系的,这个关系只有在等腰Rt三角形中四个心才能区分,而且四个心都在这个CD高线上,这样这种题目就非常快速得到解决。如果你要是能明白这个道理,那么,这次公式都不用记答案就能出来了,对于这些,我们是怎样去理解的,我们在正课里都有涉及,今天就先不说了,现在我只给大家讲述技巧,但是前提你需要把四心这个东西掌握清楚。
3、 下面我们来看一道题,要解出这道题,必须先审题,确定O是三角形的什么心,我们可以把这个三角形看做是等腰Rt三角形,把O 是什么心确定出来答案就呼之欲出了。
四个心中前三个心好理解,但唯独内心比较复杂,这个心一般在竞赛里可能会考出来,但我们平时做的高考题目一般不会给出选项,也不会给你设置东西的,即使出来选项也不是正确选项的。

4、 下面再来看一道题,来源于全国一卷的一道压轴题,同学该怎样分析呢,同样先审题,我们把它看做等腰Rt三角形,题目上点出两条边上的高的交点为H,那H就一定是垂心的,也就是说H与C重合,题目有说三角形外接圆圆心为O,那O一定是三角形ABC的中心,因为只有O到三点的距离相等才是外接圆半径,请看下图。

5、 因此对于这道高考压轴题,同学你肯定会,但是如果按照常规做,有时候同学你根本没法三到五分钟内就做出来,所以今天给大家分享的一个特别难的暗点就是向量四心问题,遇到这种题型同学就是老老实实按照这种方法去做,同学们在赋值的时候,一般赋成2,这样你会带来方便计算,这种题型也能够非常快速解决。
