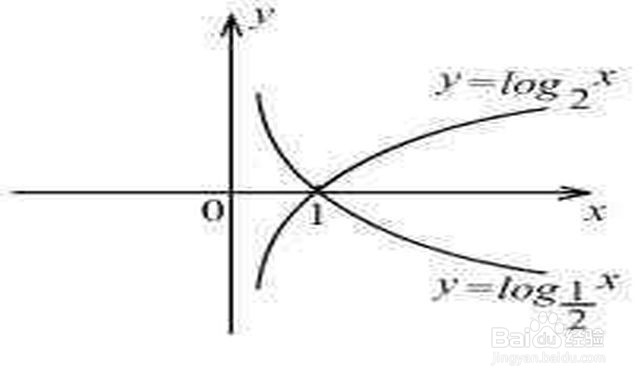
1、1.定义
如果a(a>0,且a≠1)的b次幂等于N,即ab=N,那么数b叫做以a为底N的对数,记作:logaN=b,其中a叫做对数的底数,N叫做真数。

2、2.由定义知
①负数和零没有对数;
②a>0且a≠1,N>0;
③loga1=0,logaa=1,alogaN=N,logaab=b.。
3、3.特殊对数
特别地,以10为底的对数叫常用对数,记作log10N,简记为lgN;以无理数e(e=2.718 28…)为底的对数叫做自然对数,记作logeN,简记为lnN。

4、4.对数式与指数式的互化
式子名称abN指数式ab=N(底数)(指数)(幂值)对数式logaN=b(底数)(对数)(真数)。
5、5.对数的运算性质
如果a>0,a≠1,M>0,N>0,那么
(1)loga(MN)=logaM+logaN.
(2)logaMN=logaM-logaN.
(3)logaMn=nlogaM (n∈R)。

6、6.对数的基本运算法则
①ln(x^y)=y*lnx 对数的基本运算法则
②x=e^(lnx) 。
7、7.取对数好处
缩小数据的绝对数值,方便计算。每个数据项的值都很大,许多这样的值进行计算可能对超过常用数据类型的取值范围,这时取对数,就把数值缩小了,例如TF-IDF计算时,由于在大规模语料库中,很多词的频率是非常大的数字。