1、用对数函数和函数商的求导法则等知识,介绍分式函数y=(3x+1)^2/(2x^3+2x-5)的导数的主要方法和步骤。

2、对数法求解函数y的一阶导数,主要用到对数函数的求导公式倦虺赳式,具体步骤如下。∵y=(3x+1)^2/(2x^3+2x-5),∴lny=ln(3x+1)^2/(2x^3+2x-5),即:lny=ln(泌驾台佐3x+1)2-ln(2x3+2x-5),lny=2ln(3x+1)-ln(2x3+2x-5),两边求导。

3、过程进行化简,变形即可得到一阶导数y'的最终结果。
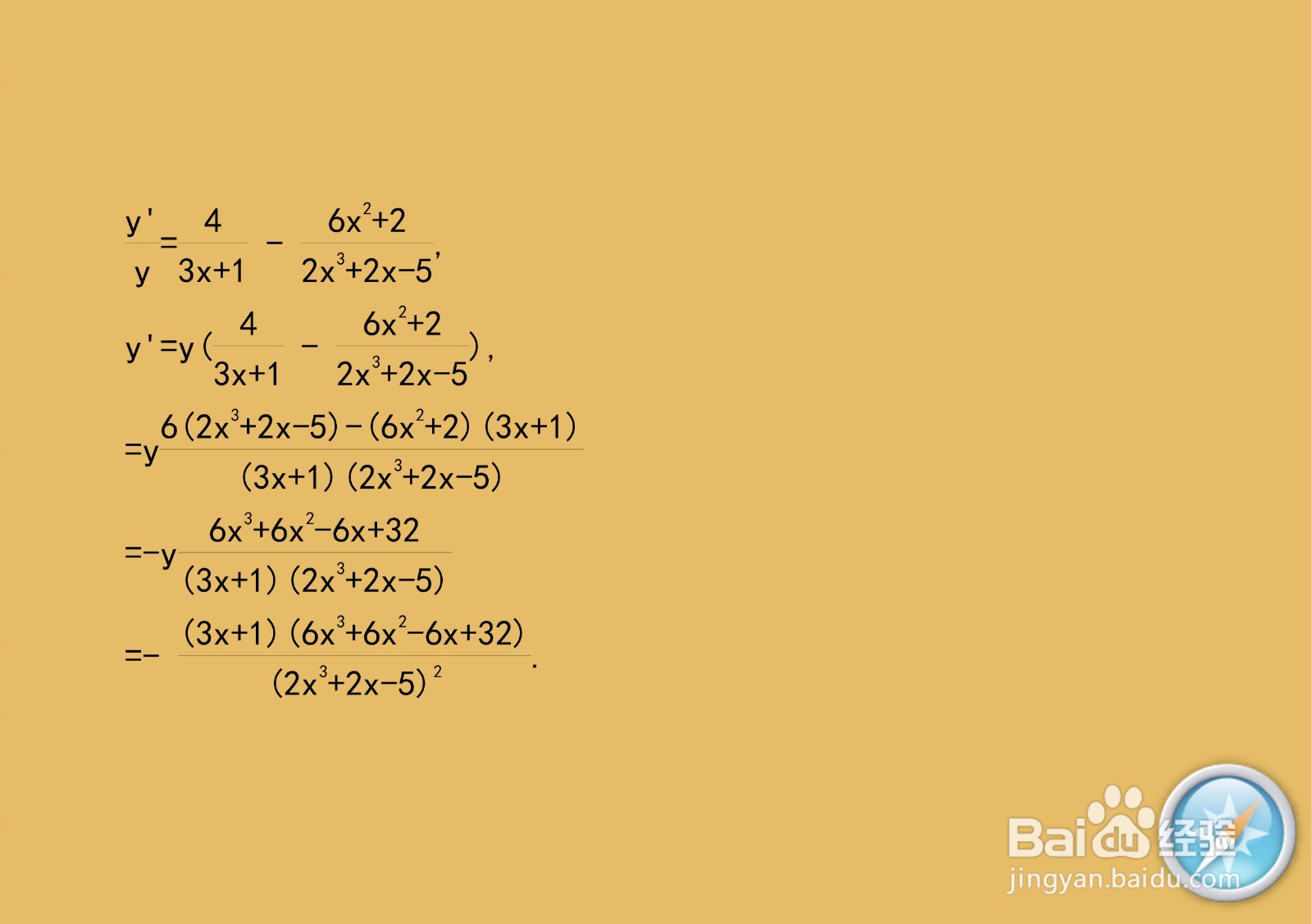
4、使用函数商的求导法则,也即可计算出函数的一阶导数。

5、利用函数乘积求导法则,计算求解函数y的二阶导数。y'(2x3+2x-5)2=(3x+1)(6x3+6x2-6x+32),设w=6x3+6x2-6x+32,则w'=18x2+12x-6,代入得:两边再次对x求导得:y"(2x3+2x-5)2+2y'(2x3+2x-5)(6x2+2x)=3w+(3x+1)w',则:y"(2x3+2x-5)2=3w+(3x+1)w'-2y'(2x3+2x-5)(6x2+2x),y"(2x3+2x-5)2=3w+(3x+1)w'+2(6x2+2x),

6、变形化简二阶导数过程,即可计算出函数的二阶导数y''.

7、再次使用函数商的求导法则,计算该函数的二阶导数y''步骤如下:u=(3x+1拘七呷憎)(6x3+6x2-6x+32),w=6x3+6x2-6x+32,v=(2x3+2x-5像粜杵泳)2,u'=3w+(2x+1)w',v'=2(6x2+2x)(2x3+2x-5),w'=18x2+12x-6,代入得:
