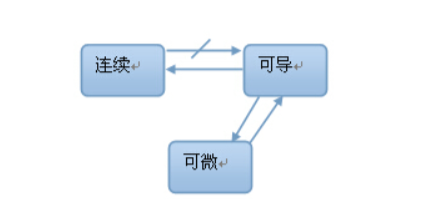
意思茧盯璜阝就是可导一定连续，连续不一定可导。
可导是连续的充分不必要条件，前半句话无需解释，后半句话很有意思，最简单的搏皋咬夼实例是y＝ |x|，在x＝0处不可导。极端地，连续函数甚至可以处处都不可导，例如魏尔斯特拉斯函数：可以直观上发现，连续但不可导是因为几何上函数图像出现了"尖角"。
拓展：
反过来，如果一个函数在某点"圆滑"，那么在该点就可导。进一步地，函数可导，但求导后的函数有可能又不可导了，也就是说，部分函数有着”导着导着就变尖了“的趋势。反过来，如果一个函数任意阶导数都可导。总结可以发现，”圆滑不圆滑“是比”连续不连续“更强的条件。
可导则连续，连续不一定可导。不连续一定不可导，具体为：连续的函数不一定可导，可导的函数是连续的函数，越是高阶可导函数曲线越是光滑。存在处处连续但处处不可导的函数。左导数和右导数存在且“相等”，才是函数在该点可导的充要条件，不是左极限=右极限。