1、 此时直线为x+2y=1,所围成的面积在第一象限,此步骤是对直线和圆位置关系进行解析。
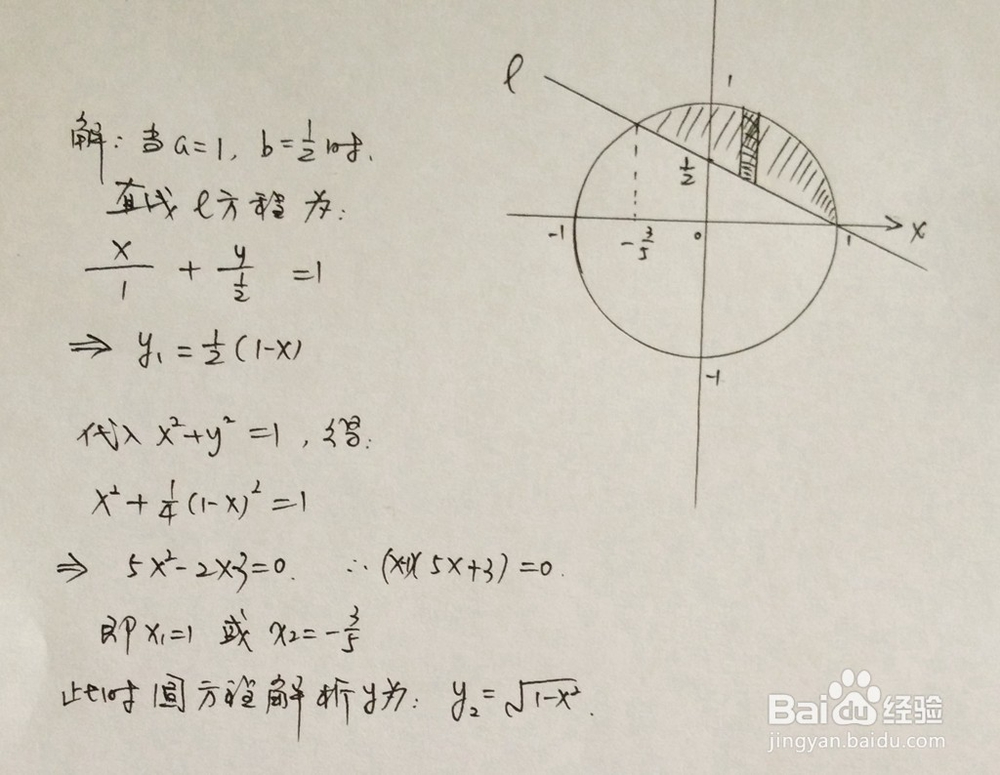
2、 定积分计算,以下为计算的主要过程。
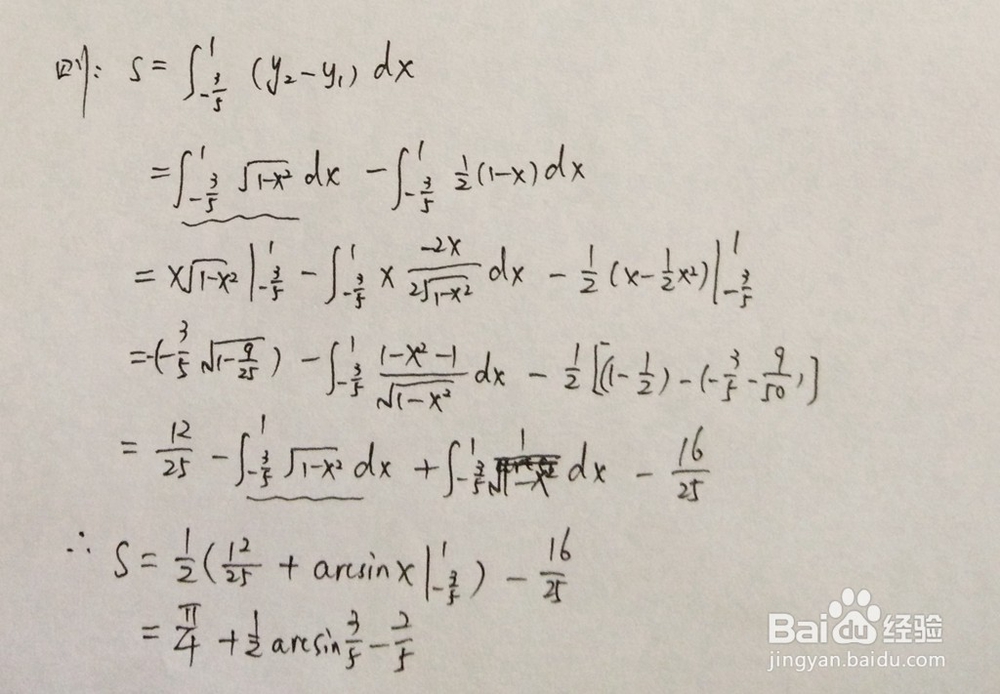
1、 此时直线为x-2y=1,所围成的面积在第四象限,此步骤是对直线和圆位置关系进行解析。

2、 定积分计算,以下为计算的主要过程。

1、 此时直线为-x+2y=1,所围成的面积在第二象限,此步骤是对直线和圆位置关系进行解析。

2、 定积分计算,以下为计算的主要过程。

1、 此时直线为-x-2y=1,所围成的面积在第三象限,此步骤是对直线和圆位置关系进行解析。
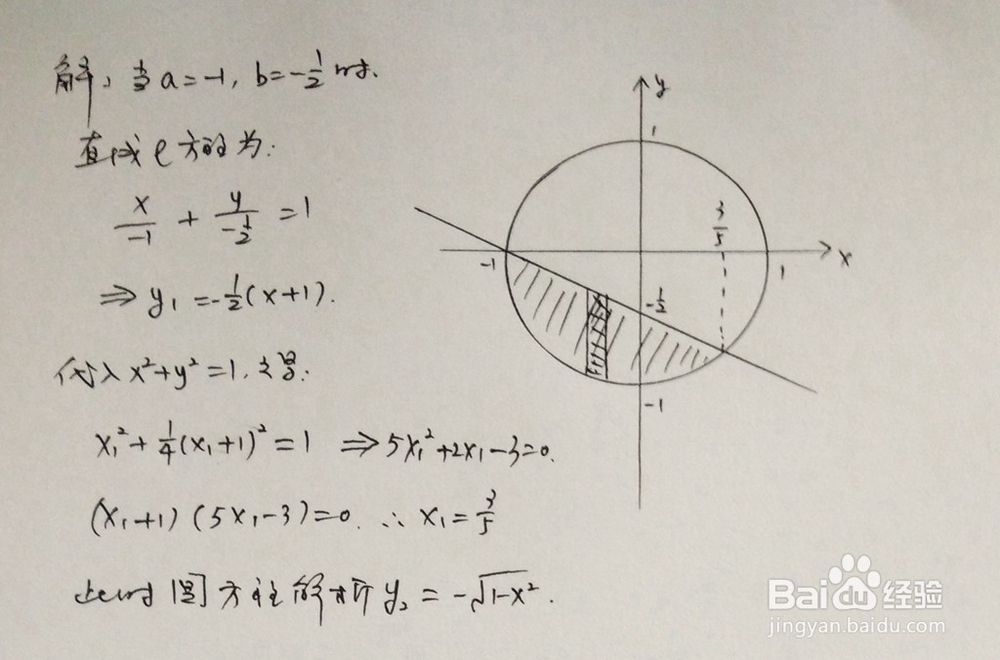
2、 定积分计算,以下为计算的主要过程。
