假设点D是三角形ABC的一个布洛卡点，满足∠DAB=∠DBC=∠DCA，B和C为定点，A为动点。若D的轨迹是圆，那么A的轨迹是什么样的？图片为高清大图，请放大查看。
工具/原料
电脑
Mathematica
网络画板
网络画板尝试
1、如果A是线段BC的垂直平分线上的动点，那么D的轨迹是圆。
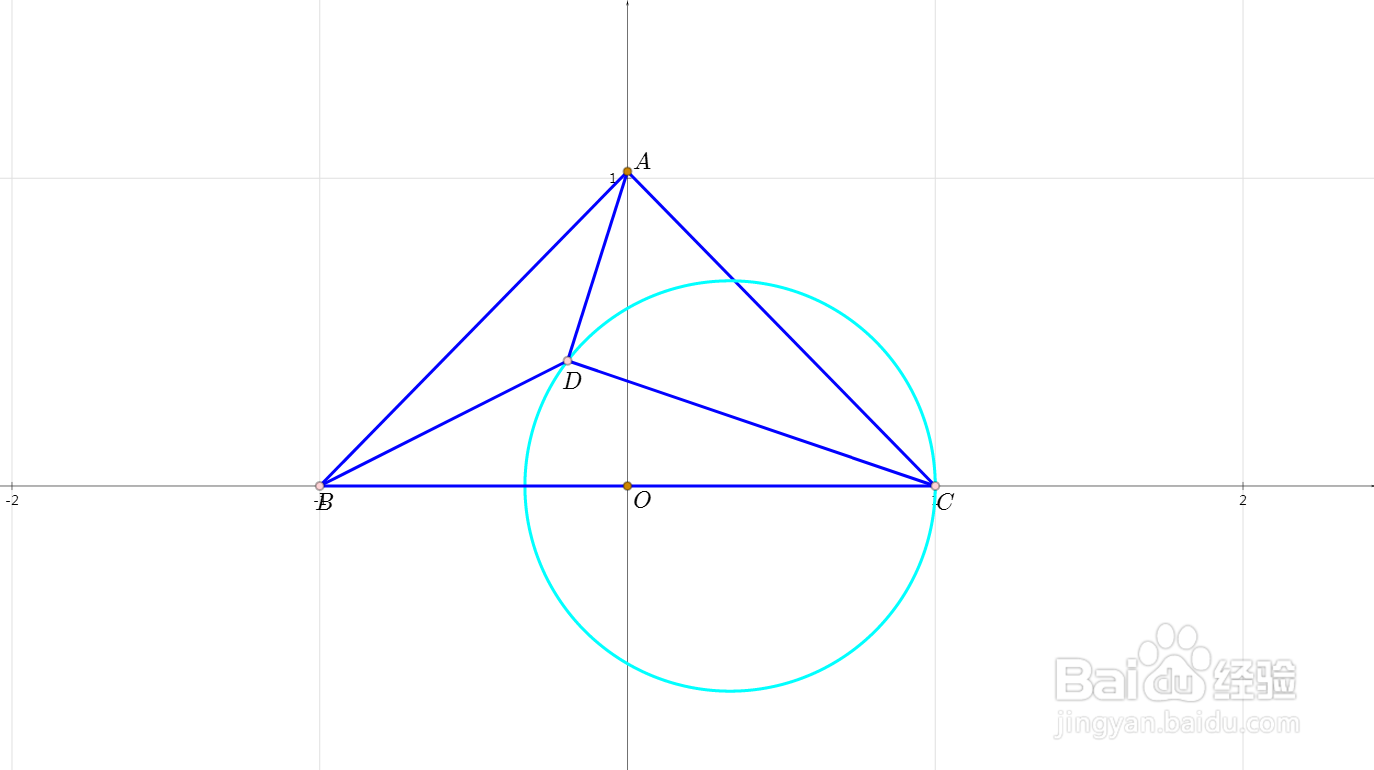
2、如果A是以B为圆心的圆上的动点，那么D的轨迹也是圆。
3、如果A是下面的四次曲线上一点，那么D的羌礤掘暑轨迹也是圆。其中，B是(-1,0)点，C是(1,0)点，四次曲线的方程式是：-9x+15x^2+9x^3+x^4+y^2+9x y^2+2 旌忭檀挢x^2 y^2+y^4=0。这个四次曲线分成了两支，如图的绿色曲线，每一支都足以确定D的轨迹圆，因此，这个轨迹圆被遍历二次。
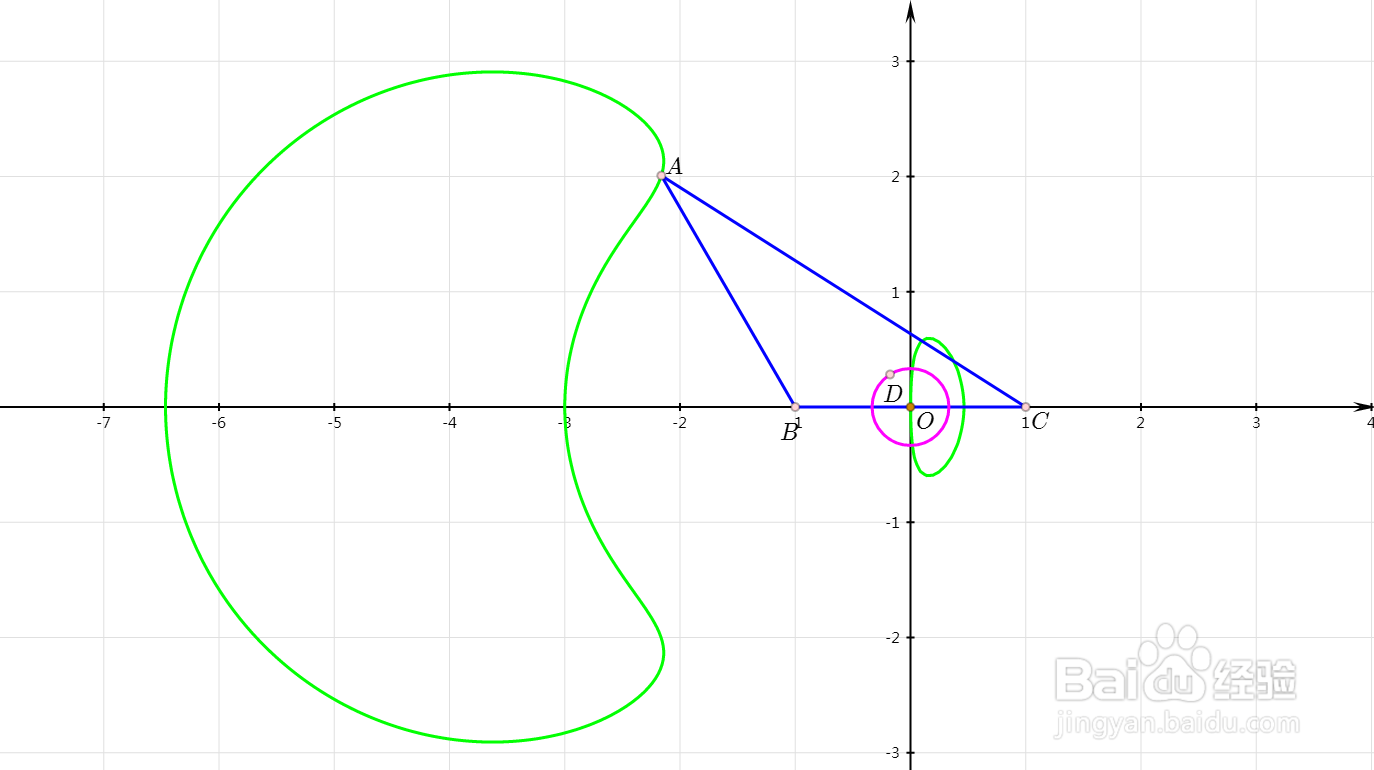
4、由此可知，如果布洛卡点的轨迹是圆，对应的A的轨迹，是十分复杂的。下面，我借助Mathematica的符号计算能力，来具体的考察A的轨迹。
Mathematica尝试
1、假设坐标：{AA, BB, CC} = {{a, b}, {-1, 0}, {1, 0}};用两个字母表示点的标签，防止与Mathematica的内置函数冲突。
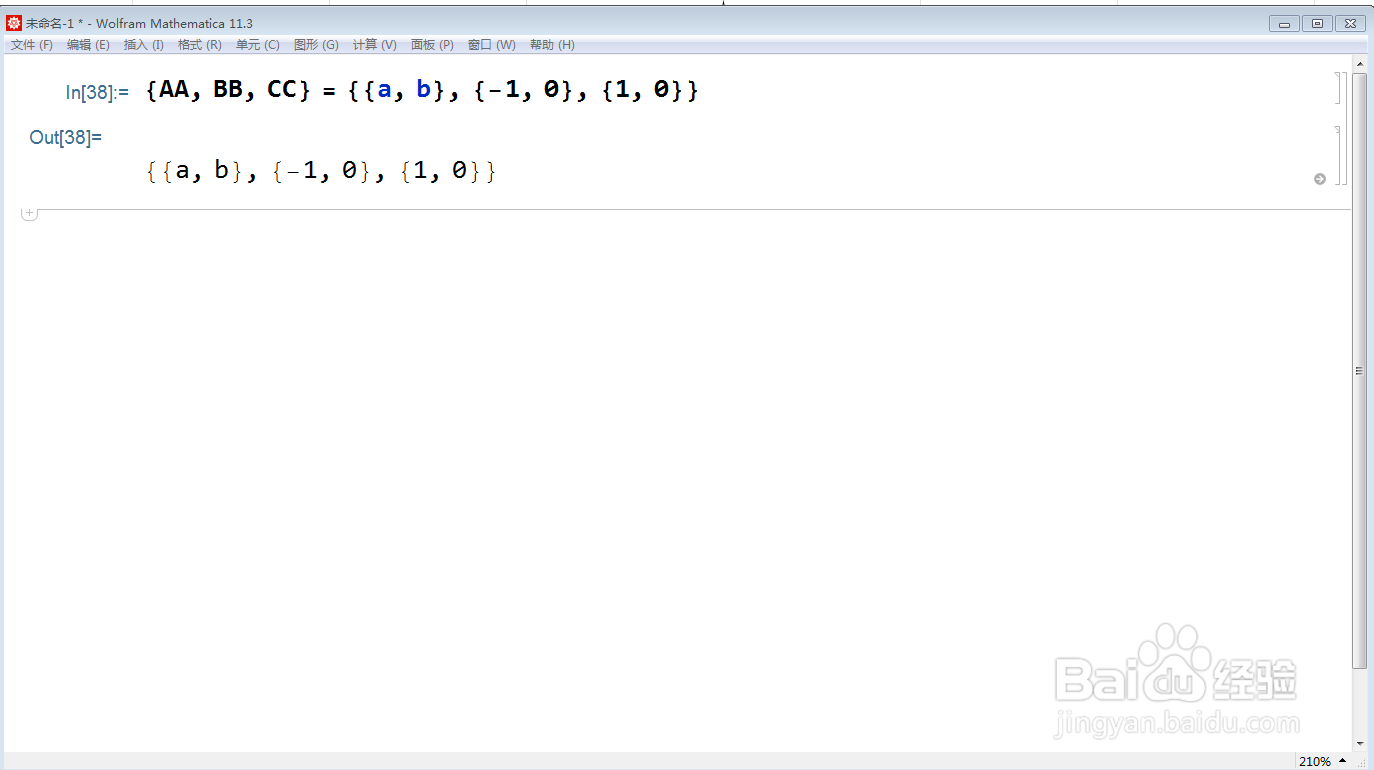
2、计算布洛卡点D的坐标：DD = buluokadian[AA, BB, CC][[1]] // Factor;
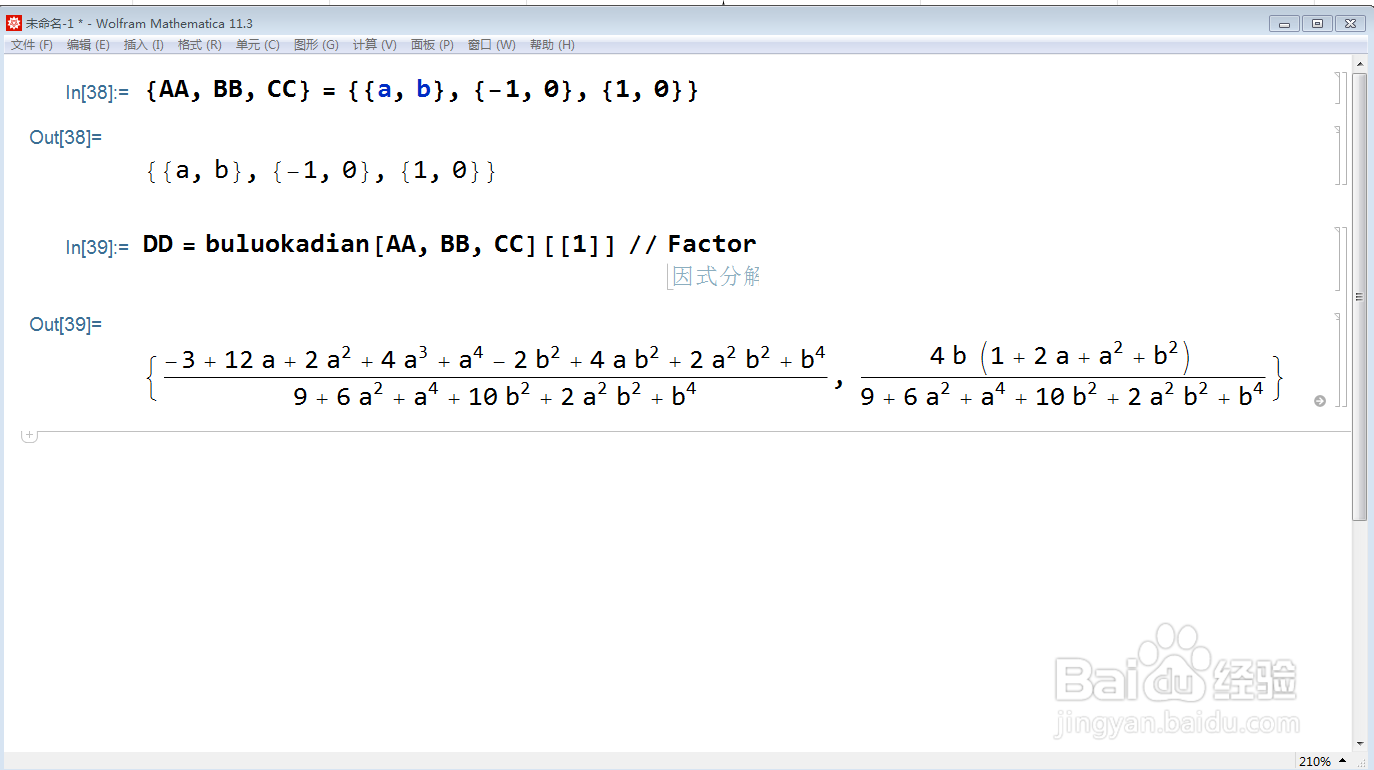
3、假设D点的轨迹是一个以(u,v)点为圆心、r为半径的圆上，也就是D到(u,v)点的距离等于r。由此，可以反过来确定a、b满足的关系式：fc0 = (DD - {u, v}).(DD - {u, v}) - r^2 // Factor // Numerator;
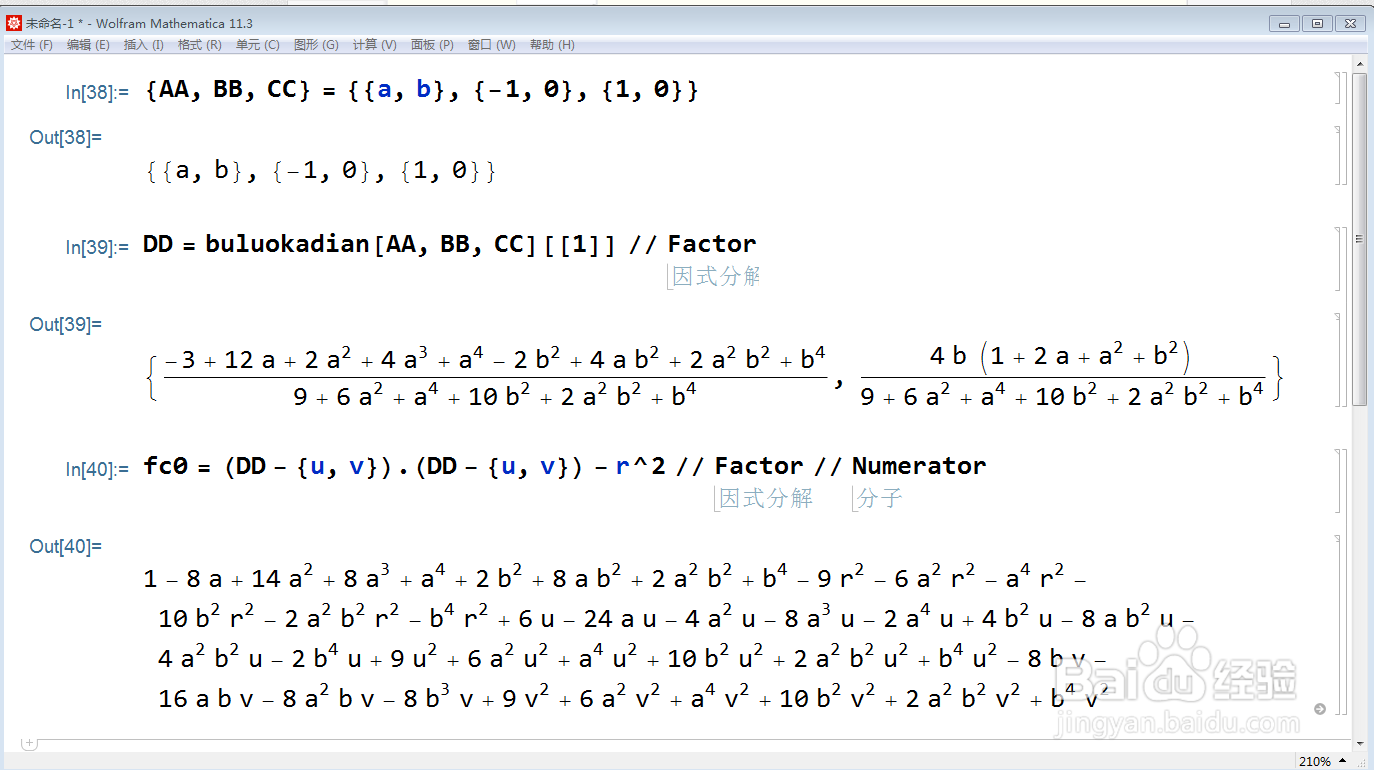
4、把上面运行结果里的a和b置换为x和y，就得到A的轨迹方程式：fc = fc0 /. {a -> x, b -> y};
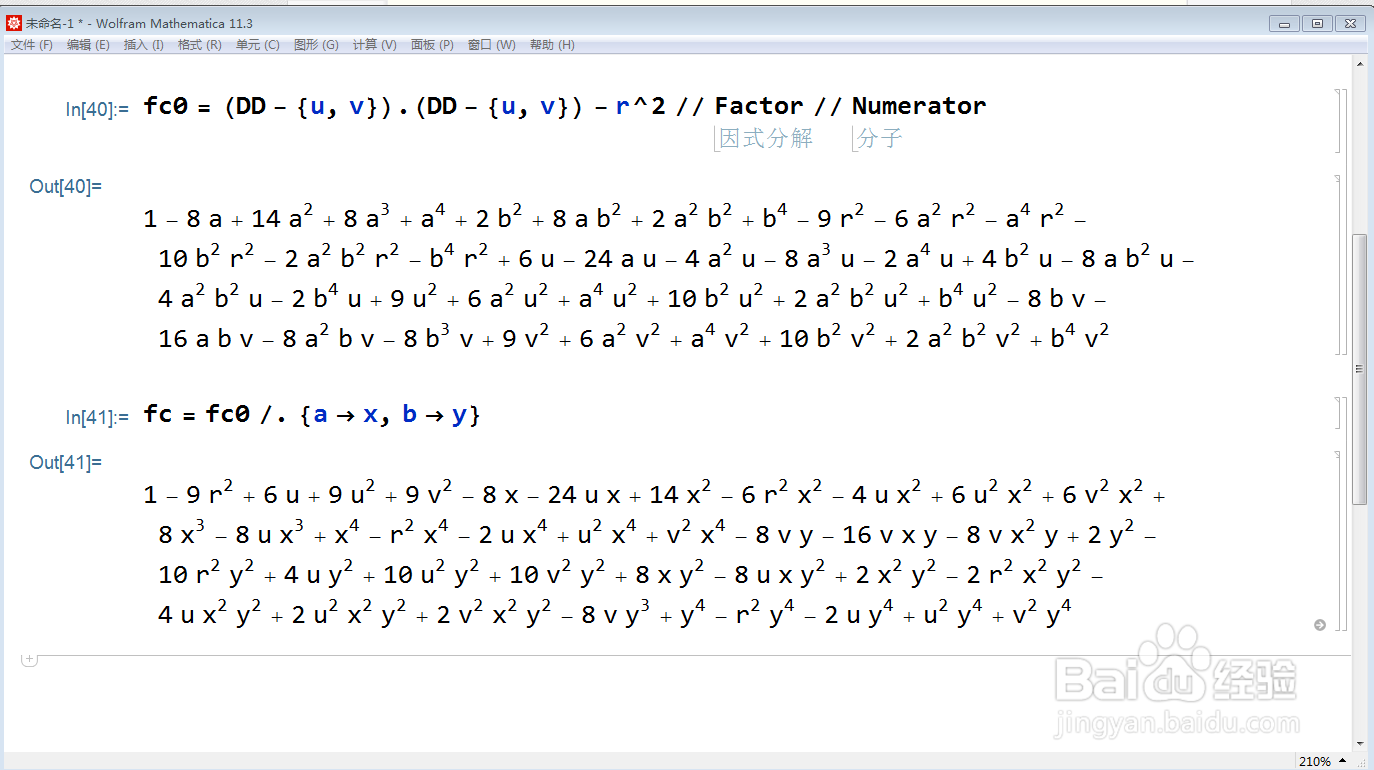
5、可以验证，A的轨迹方程式至多是一条四次曲线：fc // cishufenli // FullSimplify // Column;
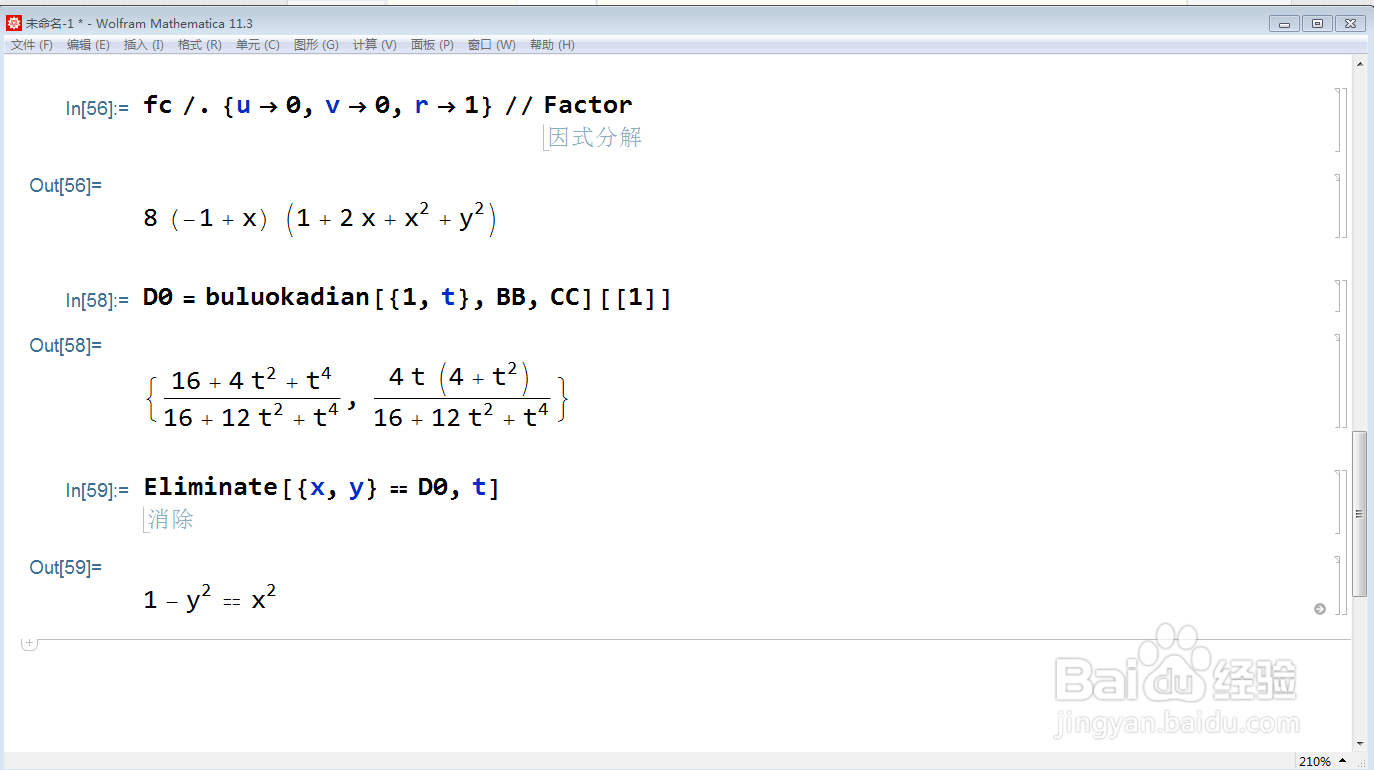
6、特别赋值：当u=0，v=0，r=1时，代表D的轨迹是撮劝丛食单位圆，此时，A的轨迹是直线x=1。注意：A的轨迹的方程式是(-1 + x) (1 + 2 x + x^2 + y^2)=0，除了x=1以外，还有一个孤立点(-1,0)，这个孤立点请忽略。
7、作为验证，网络画板作图如下。实践证明，D的轨迹仅仅是一段圆弧，而不是一个完整的圆。另外，为什么不用Mathematica作图？因为，Mathematica根据参数方程作图，得到的一定是一个完整的圆，很可能与实际不符。
