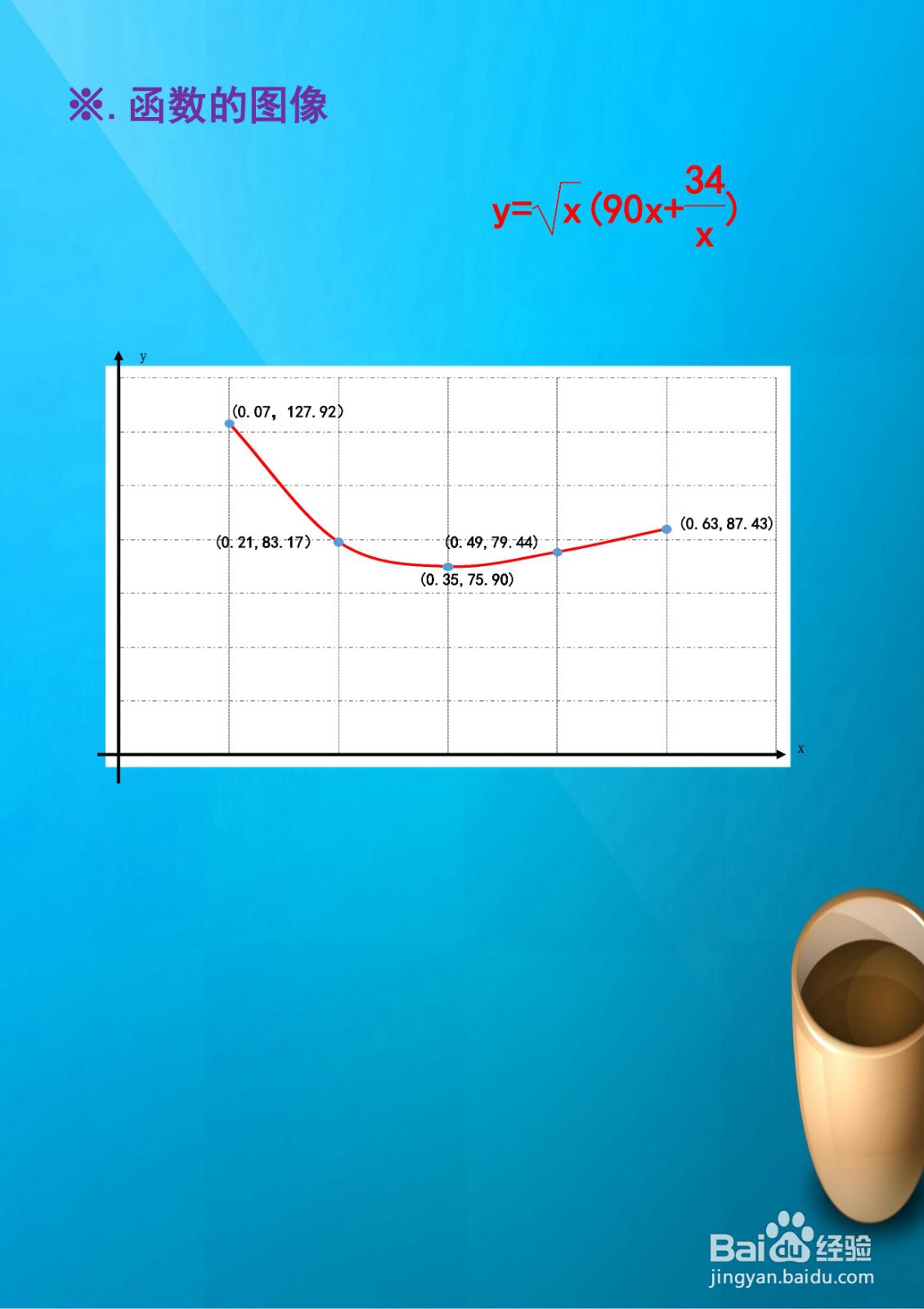
1、※.函数的定义域
∵√x有x≥0;对34/x有x≠0.∴函数的定义域为:(0,+∞)。

2、设A,B是两个非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A--B为集合A到集合B的一个函数,记作y=f(x),x属于集合A。其中,x叫作自变量,x的取值范围A叫作函数的定义域。
3、※.函数的单调性
∵y=√x(90x+34/x)
=90x^(3/2)+34x^(-1/2),对x求导得:
∴dy/dx
=(3/2)*90x^(1/2)-(34/2)x^(-3/2)
=(1/2)x^(-3/2)(3*90x²-34).
令dy/dx=0,则x²=17/135.
又因为x>0,则x=(1/45)√255≈0.35.
(1)当x∈(0, (1/45)√255)时,dy/dx<0,函数y为单调减函数;
(2)当x∈[(1/45)√255,+∞)时,dy/dx>0,函数y为单调增函数。

4、※.函数的凸凹性
∵dy/dx=(1/2)x^(-3/2)(3*90x²-34),
∴d^2y/dx^2
=-3/4*x^(-5/2)(3*90x²-34)+3*90x*x^(-3/2)
=-3/4*x^(-5/2)(3*90x²-34)+3*90x^(-1/2)
=-3/4x^(-5/2)(3*90x²-34-4*90x²)
=3/4x^(-5/2)(90x²+34)>0,则:
函数y在定义域上为凹函数。

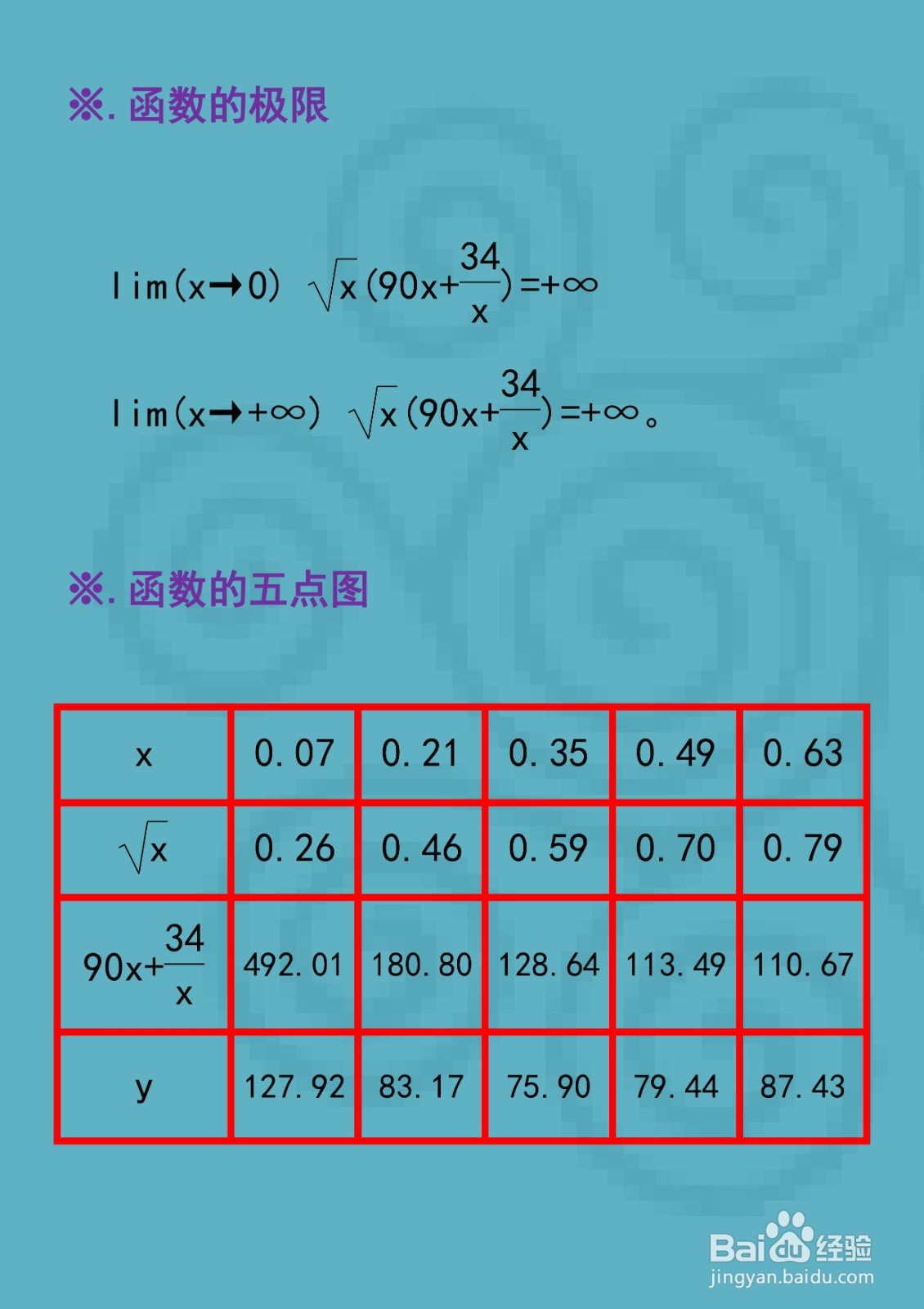
5、※.函数的极限
Lim(x→0) √x(90x+34/x)=+∞
Lim(x→+∞) √x(90x+34/x)=+∞。
6、综合以上函数的定义域、单调性、凸凹性、极限等性质,函数的示意图如下: