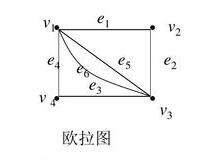
1、首先,我们要明白欧拉闭迹、欧拉环游、欧拉回路的概念以异同。其实,这三个是完全一样的概念,是完全相同的。经过每条边的闭迹就是欧拉闭迹,又叫欧拉环游或欧拉回路。其中,迹是指边不重复的途径;闭则指起点与终点重合。例如,下图就是一个欧拉闭迹。

2、接下来,我们要明白什么样的图才有欧拉环游。这是很简单的,即一个无向图存在欧拉回路,当且仅当该图所有顶点度数都为偶数,且该图是连通图。例如,下图就具有欧拉回路。

3、下面,我们要搞清楚什么叫字斤谯噌最优欧拉环游。其实,最优欧拉环游就是对一个不具有欧拉环游的图,我们想找到一条闭路径,让它经过每一条边至少一关骇脘骱次后回到起点,同时耗费的代价最小。很显然,假如这个图存在欧拉环游的话,那么总代价就是每条边的权重之和。下图中的最优欧拉环游就是e1~e6的权重之和。
4、接下来,我们要解决的是对于一个不存在欧拉环游的图,如何求其最优欧拉环游的权重。管梅谷定理就是专门为了解决这个问题而提出的。通常而言,我们遇到的图都只有两个奇度顶点u,v,这种情况分为3步:1. 求出u,v之间的最短路,记最短路权重之和为w1;2. 将最短路加上平行边,得到图G*;3. 用Fluery算法求G*的欧拉环游,即为G的最优欧拉环游。

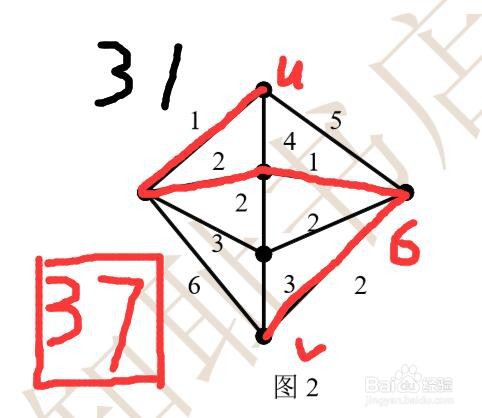
5、最后,我们就可以得到最优欧拉环游问题的结论啦。最优欧拉环游的权重就是两个奇数度顶点u,v之间最短路的权重w1与整个图总权重w2之和。例如,图中的答案就是37.其中最短路权重为6;整个图权重是31,加起来就是37啦。