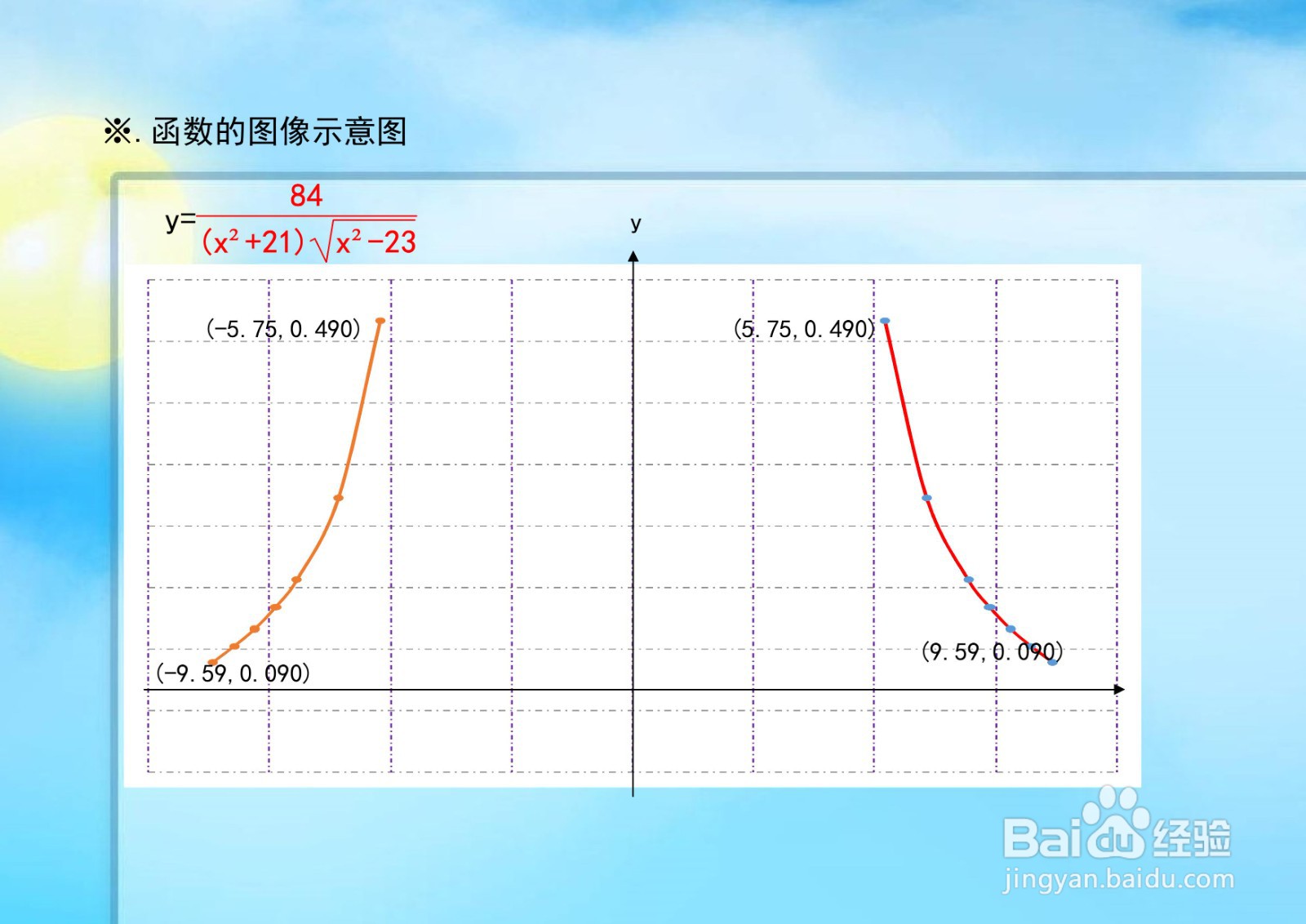
1、根据函数特则解析函数的定义域,由于函数为分式函数,且含有根式,即可求自变量的取值范围,则为函数的定义域。

2、函数的定义域是函数的三要素(定义域、值域、对应法则)之一,指函数自变量的取值范围。具体来说,对于两个存在函数对应关系的非空集合D、M,如果集合D中的任意一个数,在集合M中都有且仅有一个确定的数与之对应,则集合D称为函数的定义域。
3、利用函数的导数知识,计算函数的一阶导数,得到函数的驻点,判断函数的单调性,并求出函数的单调区间。

4、解析函数的凸凹性,利用函数的导数知识,计算函数的二阶导数,判断函数的凸凹性,并求出函数的凸凹区间。
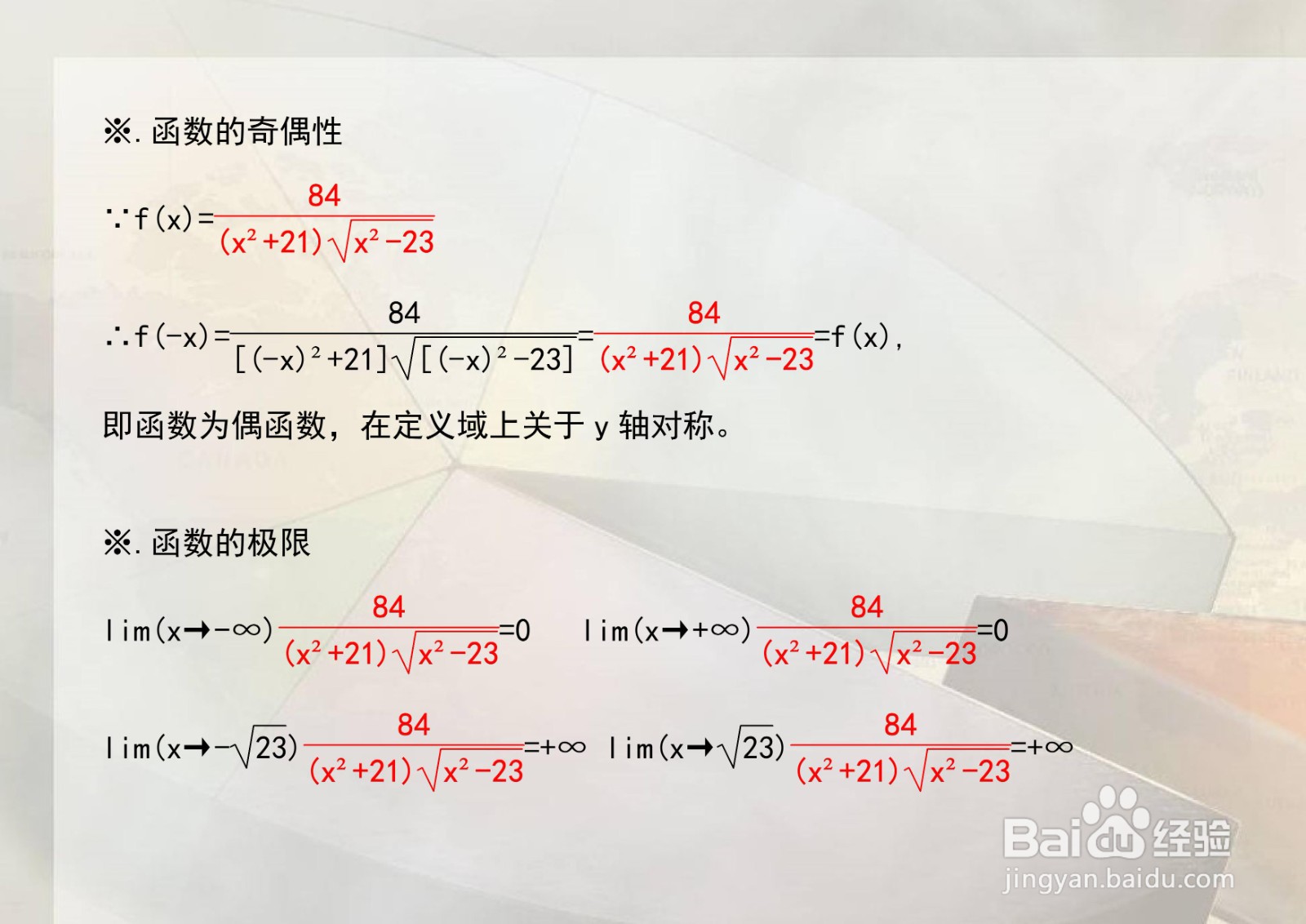
5、函数上的五点示意图如下:
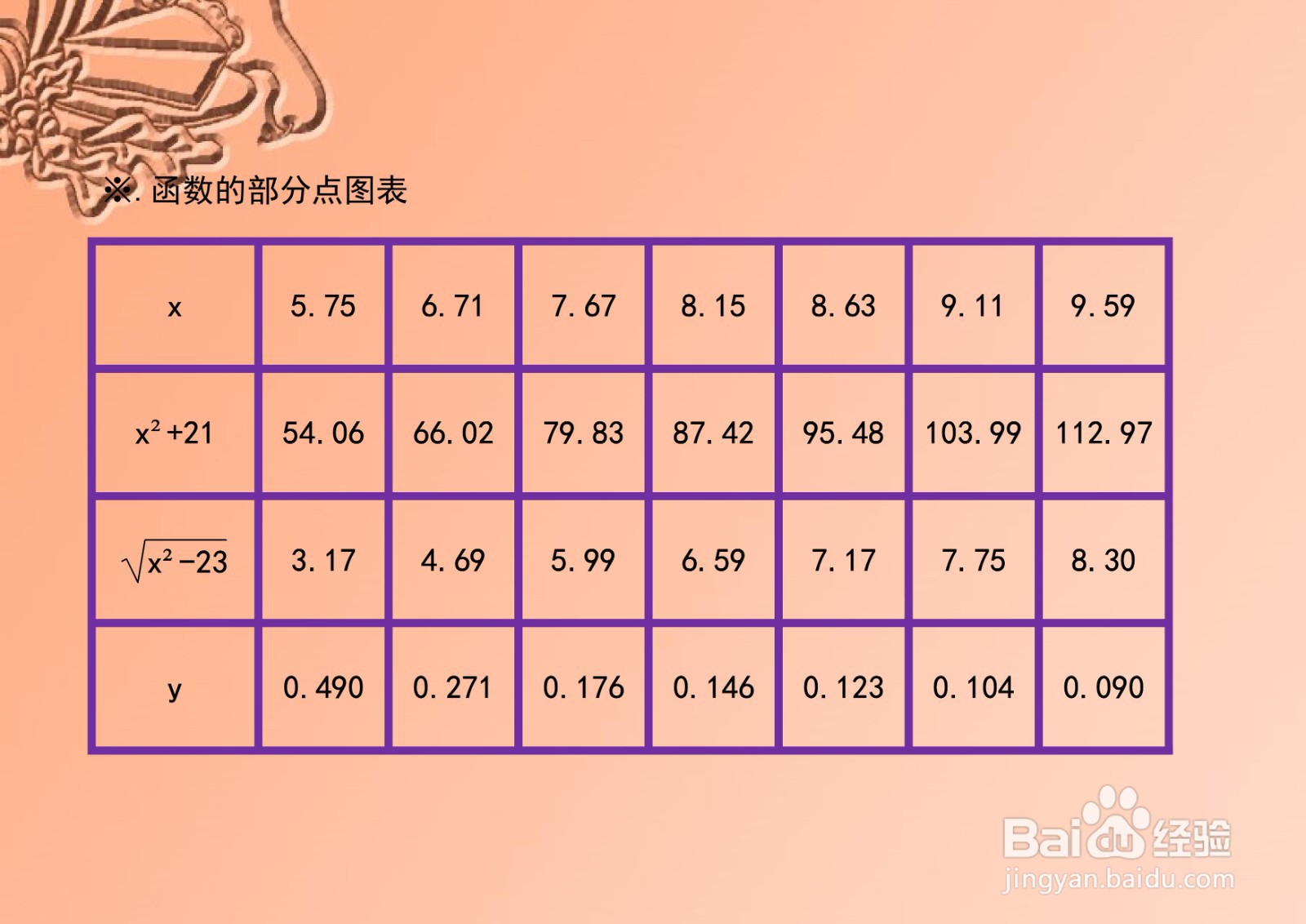
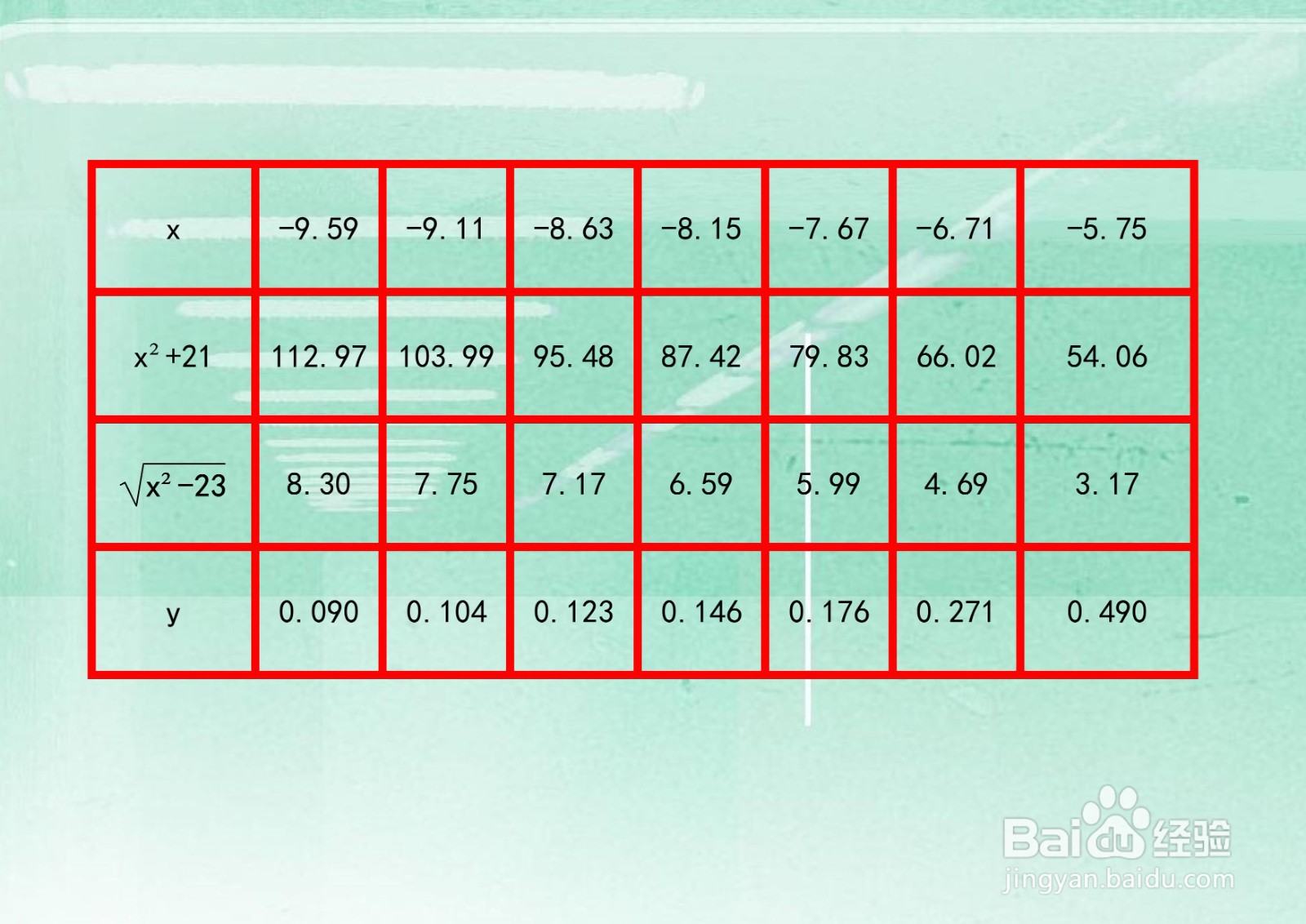
7、综合以上函数的定义域、值域、单调性、凸凹性和极限等性质,函数的示意图如下: