1、LU 分解(或高斯消去法)将任何方阵 A 都表示为下三角矩阵和上三角矩阵的置换之积A = LU ,其中,L 是对角线元素为 1 的下三角形矩阵的置换,U 是上三角形矩阵。出于理论和计算原因,必须进行置换。矩阵
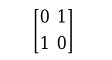
2、在不交换其两行的情况下不能表示为三角矩阵的积。尽管矩阵

3、可以表示为三角矩阵之积,但当 ε 很小时,因子中的元素也会很大并且会增大误差,因此即使置换并非完全必要,它们也是所希望的。部分主元消元法可确保 L 的元素的模以 1 为限,并且 U 的元素并不大于 A的元素。例如:[L,U] = lu(B)

4、通过对 A 执行 LU 分解,可以A*x = b使用以下表达式快速对线性方程组求解x = U\(L\b)行列式和逆矩阵是通过 LU 分解使用以下表达式进行计算的det(A) = det(L)*det(U)和inv(A) = inv(U)*inv(L)也可以使用 det(A) = prod(diag(U)) 计算行列式,但行列式的符号可能会相反。