1、梯度向量:
定义:
目标函数f为单变量,是关于自变量向量x=(x1,x2,…,xn)T的函数,
单变量函数f对向量x求梯度,结果为一个与向量x同维度的向量,称之为梯度向量;
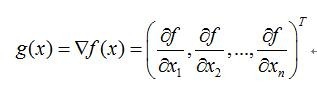
2、Jacobian矩阵:
定义:
目标函数f为一个函数向量,f=(f1(x),f2(x),…fm(x))T;
其中,自变量x=(x1,x2,…,xn)T;
函数向量f对x求梯度,结果为一个矩阵;行数为f的维数;列数位x的维度,称之为Jacobian矩阵;
其每一行都是由相应函数的梯度向量转置构成的;
【注】:梯度向量Jacobian矩阵的一个特例;
当目标函数为标量函数时,Jacobian矩阵是梯度向量;

3、Hessian矩阵:
实际上,Hessian矩阵是梯度向量g(x)对自变量x的Jacobian矩阵:

4、内积:
向量a和向量b的内积等于a的长度乘b的长度乘夹角的余弦;

5、海森矩阵在牛顿法中的应用
牛顿法主要应用在两个方面:求方程的根; 最优化;
1)求解方程:
并不是所有的方程都有求根公式, 或者求根公式很复杂, 导致求解困难;
利用牛顿法, 可以迭代求解;
原理:
利用泰勒公式, 在x0处一阶展开,即f(x)=f(x0)+(x-x0)f’(x0);
求解方程f(x)=0,即f(x0)+(x-x0)f’(x0)=0, 求解x=x1=x0-f(x0)/f’(x0),
因为利用泰勒公式的一阶展开, f(x)=f(x0)+(x-x0)f’(x0)处是近似相等;
f(x1)的值比f(x0)更接近f(x)=0,于是迭代求解;
推出xn+1=xn–f(xn)/f’(xn)通过迭代, 这个式子必然在f(x^∗)=0的时候收敛;
整个过程如下图:

6、2)最优化:
在最优化的问题中,
线性最优化可以用不动点算法求解,
但非线性优化问题, 牛顿法提供了一种求解的办法;
假设优化一个目标函数f, 求函数f的极大极小问题,可转化为f’=0的问题;
把优化问题看成方程求解问题(f’=0);
求解f’=0的根, 把f(x)的2阶泰勒展开:
f(x+Δx)=f(x)+f’(x)Δx+1/2f’’(x)Δx^2;
当且仅当Δx 无限趋近于0时, f(x+Δx)=f(x)约去这两项,
对余项式f’(x)Δx+1/2f”(x)Δx^2=0对Δx求导(注: f’(x), f’’(x)均为常数项;
此时上式等价:
f’(x)+f’’(x)Δx=0;
求解:
Δx=−f’(xn)/f’’(xn);
得出迭代公式:
xn+1=xn−f’(xn)f’’(xn),n=0,1,...
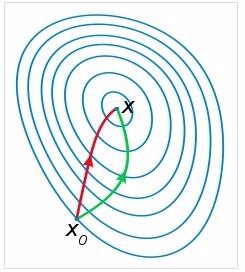
一般认为牛顿法可以利用到曲线本身的信息, 比梯度下降法更容易收敛(迭代更少次数),
如下图是一个最小化一个目标方程的例子, 红色曲线是利用牛顿法迭代求解, 绿色曲线是利用梯度下降法求解;