本篇经验介绍一种典型非周期信号——单边指数信号的傅里叶变换求解与作图，傅里叶变换采用解析法，作图软件使用MATLAB。
工具/原料
MATLAB，版本：R2018a
纸笔
单边指数信号作图
1、在信号与系统中，单边指数信号，默认是单边指数衰减信号，其定义如下图a所示。在MATLAB中作出对应的函数散点图，如图b。
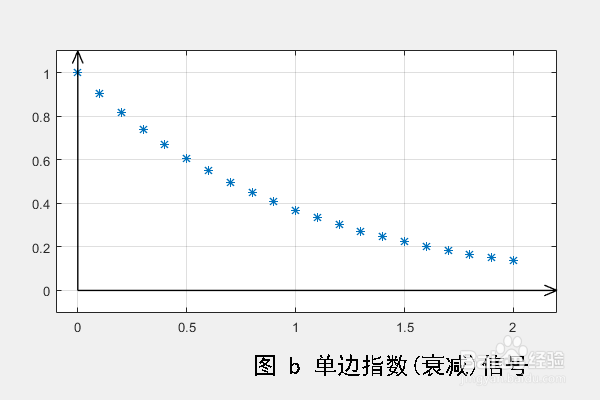
2、图b对应的参数a为1，MATLAB作图代码如下：clearclca = 1;t = 0: 0.1 :2;y = exp(-a*t);plot(t, y, '*');axis equalhold onset(gca, 'XLim', [-0.1, 2.2]);set(gca, 'XTick', 0:0.5:2.2);set(gca, 'YLim', [-0.1, 1.1]);set(gca, 'YTick', 0:0.2:1.1);plot([0 2.2], [0 0], 'black', 'LineWidth', 1);add_arrow_to_line(0, 2.2, 0, 0, 'black', 1);plot([0 0], [0 1.1], 'black', 'LineWidth', 1);add_arrow_to_line(0, 0, 0, 1.1, 'black', 1);grid onhold off
采用解析法求单边指数信号的傅里叶变换
1、采用解析法求单边指数信号的傅里叶变换，即将单边指数信号乘以exp(-jwt)后在定义域内对t进行积分，该过程及结果如图d所示。
2、将参数a等于1代入图d所求得的傅里叶变换后幅度公式，在MATLAB中作出对应的幅度谱，如图e所示。
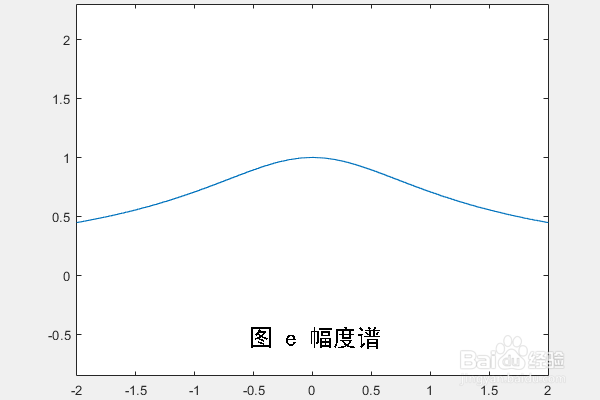
3、将参数a等于1代入图d所求得的傅里叶变换后相位公式，在MATLAB中作出对应的相位谱，如图f所示。
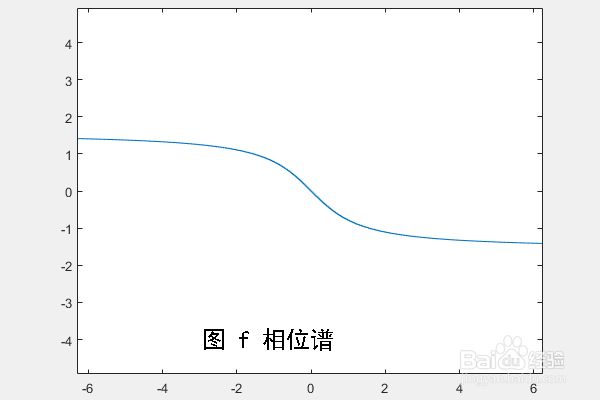
4、给出生成单边指数信号幅度谱和相位谱的MATLAB代码如下：clearclc%% 相位谱w = -2: 0.1 :2;y = 1./sqrt(1+w.*w);figure(1);plot(w, y);axis equal%% 相位谱w = -2*pi: 0.1 :2*pi;y = -atan(w);figure(2);plot(w, y);axis equal
