1、一.直线方程与椭圆方程的联立——设y=kx+b，再用韦达定理Ps. 1)为了防止把b看成6，一般设y=kx+m 2)定点（0，m）在y轴上，设直线为y=kx+m。定点（n，0）在x轴上，设直缏堋垌胯线为x=ky+n。利于联立方程的求解 3)变换直线方程的形式，对合求解通常对合解法常与坐标轴的平移，斜率的相乘相加有关，但相对于极坐标和参数方程略显复杂
2、圆的诸多性质——仿射基础1)切割线定理2）相交弦定理（多次遇见不做详细解释）3）垂径定理：垂直于弦的直劐孕瞬腊径平分弦且平分这条弦所对的两条弧。4）扇形面积：（类比三角形的底称高除以二）弧长乘半径除以二，S= 0.5LR5）阿波罗尼圆Apollonius：平面内到两个定点的距离之比为常数k（k≠1）的点的轨迹是圆，这个圆就是阿波罗尼圆。已知：定点M（c,0），N（-c,0），P（x，y）求证：平面内到两个定点M，N的距离之比为常数k（k≠1）的点P的轨迹是圆证明：d1比d2=k（d用点到点距离公式带）通分后化简得(k²-1)x²+(k²-1)y²+(k²+1)x+(k²-1)c²=0约分 x²+y²+(k²+1)/(k²-1)x+c²=0此形式为圆的一般方程。
3、三.参数方程的用法参数方程一般联立时切勿使用，因为一个cos，sin下来，答题纸就不够写的了抛物线一般设直方最简单，不用参数参数方程最大的好处就是求范围比较舒服，而且式子中的转化比较明显。
4、四，点差法——高中最有用的方法相比起一些不靠谱的神技能，点差法可谓是圆锥曲线官方认可的一个大bug
5、五.极点极帧霭绎郎线的用法和性质——站在出题人的角度思考答案定义： 对于二次曲线C：Ax²+By²+Cx+Dy+E=0和一点P（x0，y0） 其中A²+B²≠0，P不在曲线的中心和渐近线上 用x0*x沪枭诽纾代x²，yo*y代y²，（x0+x）/2代x，（yo+y）/2代y，得到一条直线方程 则称点P和直线l是关于曲线C的一对极点和极线 即点P是直线l关于曲线C的极点，直线l是点P关于曲线C的极线。 特殊的，焦点和准线是曲线的一对特殊的极点和极线
6、其实，圆与椭圆的切线与渐切线就是特殊的极线，如图
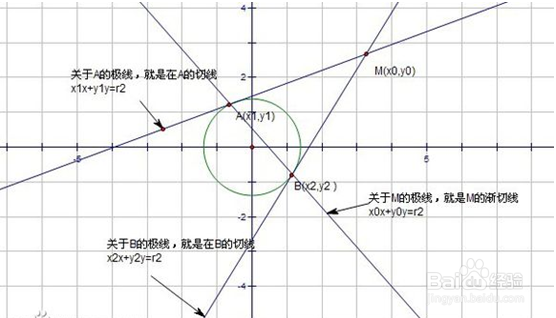
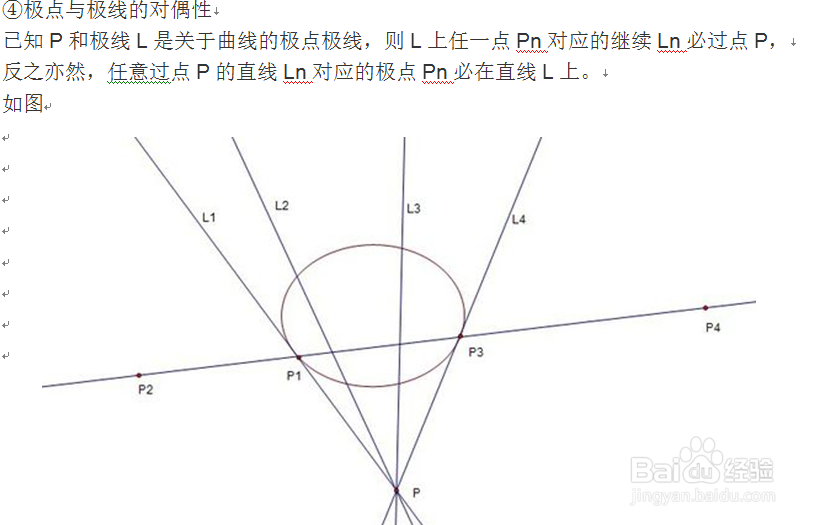
7、极点极线的性质： 一般的有如下性质（焦点所在区域为曲线内部）Ps.学完极点极线后两个毛病 1.知道是极点极线就不想算了 2.啥题型都往极点极线靠
8、六.仿射在圆锥曲线的妙用1.椭圆如何化圆？
9、七，极坐标与圆锥曲线的结合
10、八，特殊公式
11、九，圆锥曲线的几何意义
12、补充：椭圆内最大矩形面积为2ab(可用仿射法推导)。双曲线焦点到渐近线距离为b