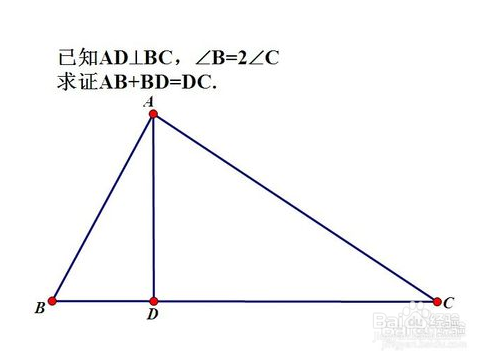
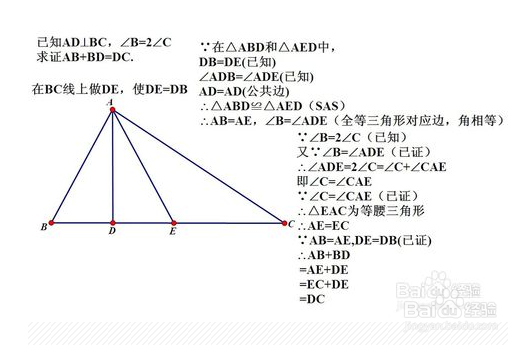
1、经过翻转、平移、对折后,能够完全重合的两个三角形叫做全等三角形,而该两个三角形的三条边及三个角都对应相等。全等三角形的性质及判定是初中数学重要的几何内容之一,为培养学生几何证明意识、逻辑推理能力起到了至关重要的作用。判定两个三角形全等一般用边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS),而特殊的直角三角形的也可以用斜边、直角边(HL)来判定。
2、在运用以上方法证明三角形全等时,往往还存在这样一个问题,条件怎么找?
在此给予一定的分析,一般而言,条件来源无非以下四种情况:
1、题目已知;比如题目直接告知一组边相等或一组角相等。

3、图中隐含;如公共边、公共角、对顶角等。
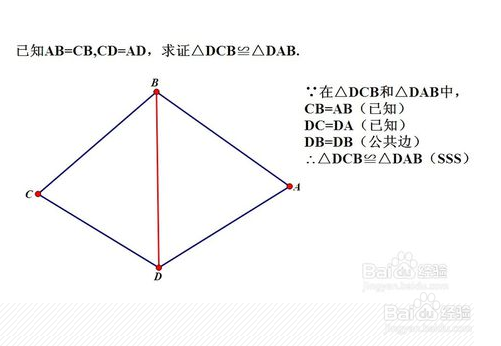
4、简单推理;比如题目中给出的已知条件往往不能直接作为三角形全等的条件,但根据已知条件(定义、定理、基本事实等)推出的结论却可以作为三角形全等的条件。
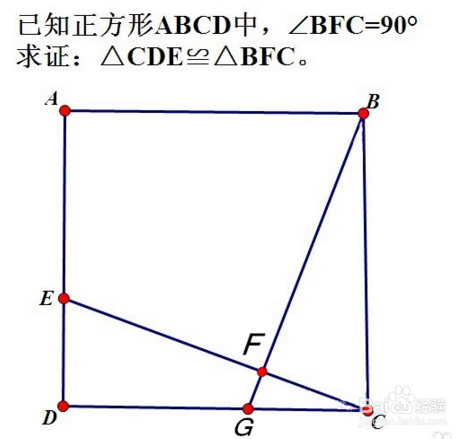

5、作图创造。比如根据以上三种方法依然无法找到说明三角形全等的条件,就需要添加辅助线来作图创造条件了。