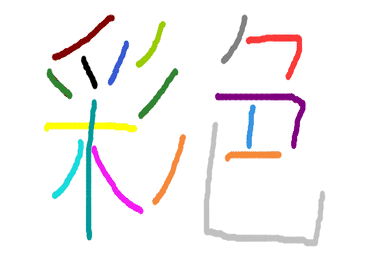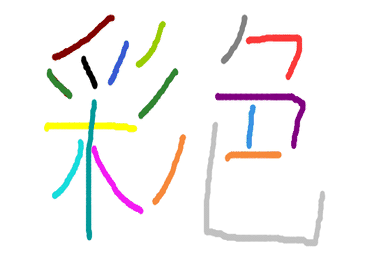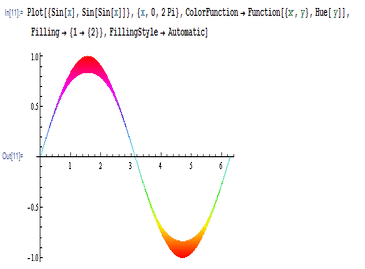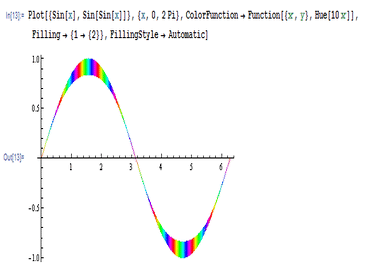1、 这里,先温习一下如何绘制各种函数的图像。 先绘制两条显函数的图像:y=sinx和y=sin(sinx),这个直接用Plot函数就可以。 再绘制两条隐函数的图像:x^4 + x^2 y^2 + y^4=1和x^4 + x^2 y^2 + y^4=2,这个要用ContourPlot函数。具体的,请参考《Mathematica绘制函数图像—隐函数图像》。

2、 这里讲怎么把不同的图像绘制在同一幅图里,这里用的命令函数是Show。Show[y1, y2, PlotRange -> {{0, 2 Pi}, {-1, 1}}]Show[x1, x2] Graphics[{x1, x2}]不能运行,理由是,x1和x2不是Graphics的图元和指令,不明就里!

3、 在两条曲线之间添加不同的颜色,使之形成一个区域;这里尝试着用RegonPlot来绘制: 隐函数的情形相对简单一些,而显函数的情形就很复杂,直到最后也没有成功。最终发现,如果两条曲线不想交,可以使用RegonPlot,但是当两条曲线相交的话,RegonPlot就无能为力了。毕竟,RegonPlot是用来绘制二元不等式(组)的区域的。

4、 经过查询,发现一个直接填充颜色的命令函数——Filling。Filling可以在指定的区域里面填充颜色,比如上面的相交曲线之间的区域,就可以用这个函数命令,看下图里面的代码。 这段代码改编自知乎,作者是Cao Hong Yang。但我个人认为这段代码有点罗索。

5、 上面的代码有点罗索,所以我在Mathematica的教科书里,自学了一下Filling的用法: Filling -> {1 -> {2}}表示在第一条曲线到第二条曲线之间的区域着色; Filling -> {1 -> Axis}表示在第一条曲线到x轴之间的区域着色。 简单的代码如下:

6、 在两条曲线之间填充各种颜色: 如图一,在两条曲线之间填充红色; 如图二,在曲线1和2之间着色,当曲线1在曲线2上面时为绿色,当曲线1在曲线2下面时为红色; 如图三,用FillingStyle来指定着色的颜色; 如图四,用透明度为0.5的蓝色填充两条曲线到x轴之间的区域,但是由于曲线sin(sinx)到x轴之间的区域被填充了两次,透明度叠加为1,所以不透明。 图一、图二、图三、图四都在下面的动态图里。

7、 用ColorFunction把曲线之间的颜色设置为色彩变换的状态,并导出动态图如下: