MATLAB教学视频:MATLAB实现连续时间系统的状态空间分析,本期视频时长约90分钟,通过具体的案例,详细地讲解了使用MATLAB创建并求解,连续时间系统的状态空间模型;着重讲解了基于系统的传递函数/微分方程,在MATLAB中实现状态空间模型的创建和求解,以及求解对应状态变量初值的具体方法。
工具/原料
MATLAB
Signal Process Toolbox
MATLAB教学视频:MATLAB实现连续时间系统的状态空间分析
1、教学内容1. 研究对象和研究目的2. 连续时间系统的状态空间模型:LCR电路案例分析3. MATLAB实现状态空间模型的创建与求解4. 状态空间模型的创建与求解:基于系统微分方程/传递函数5. 补充与扩展5.1 状态变量初值问题5.2 逆矩阵问题


2、研究对象和研究目的使用MATLAB实现连续时间系统的状态空间分析,求解连续时间系统状态空间模型,在确定性输入信号(激励信号)的作用下,对输入信号的响应 (系统的输出)1. 连续时间线性时不变系统 (LTI system)2. 本课程只讨论单输入单输出系统 (SISO system)3. 多输入多输出系统 (MIMO system) 的分析方法,可由单输入单输出系统进行类比和引申4. 视频:连续时间系统的时域分析,lsim 函数只用来求解系统的零状态响应 (基于传递函数)5. 使用 lsim 函数求解系统的全响应和零输入响应,需要基于系统的状态空间模型

3、连续时间系统的状态空间模型 (State -Space Model)为了与MATLAB里的相关函数的定义说明保持一致,约定以下符号1. 输入信号 (激励信号): u(t)2. 输出信号 (系统响应): y(t)3. 系统的状态矢量: x(t)

4、案例分析——LCR电路通过引入状态变量,将二阶微分方程描述的系统,改由一阶微分方程组来描述





5、MATLAB实现状态空间模型的创建与求解1. 连续时间系统的状态空间模型sys_ss的创建1.1 sys_ss= ss(A, B, C, D)1.2 根据系统微分方程/ 传递函数求得2. MATLAB提供了一个强大的lsim函数,用于求解系统的状态空间模型基本调用格式:y = lsim(sys_ss, u, t, x0) & [y, t, x] = lsim(sys_ss, u, t, x0)

6、状态空间模型求解:LCR电路模型

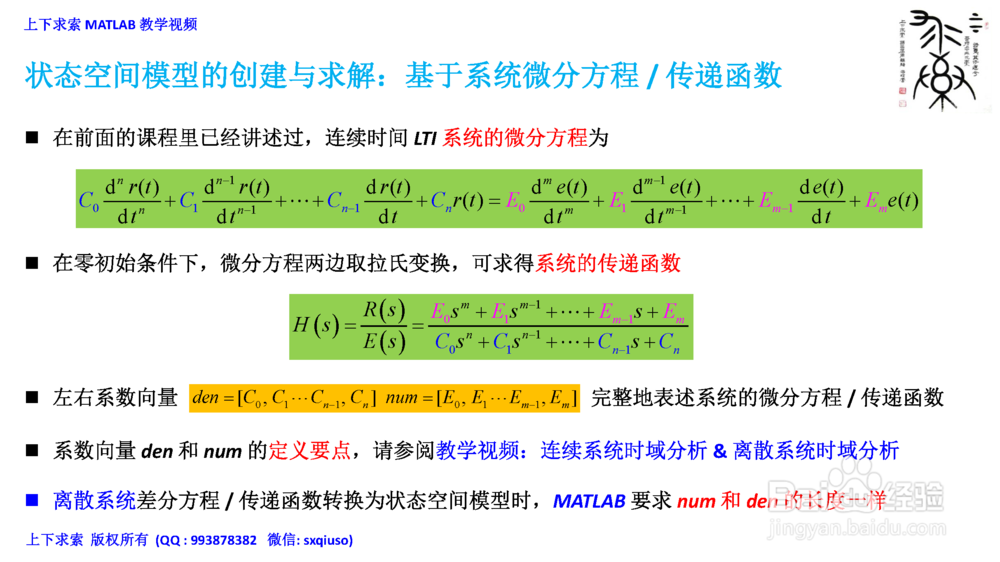
7、状态空间模型的创建与求解:基于系统微分方程/ 传递函数1.系数向量den 和num的定义要点,请参阅教学视频:连续系统时域分析& 离散系统时域分析2.离散系统差分方程/ 传递函数转换为状态空间模型时,MATLAB要求num和den 的长度一样3. 根据系统的微分方程/ 传递函数,创建状态空间模型4.直接由系数向量生成状态空间模型5.先由系数向量,定义出系统的传递函数,再转换成状态空间模型6.状态空间模型转换为系统微分方程/ 传递函数






8、补充与扩展:状态变量初值问题连续时间系统的全响应= 零状态响应+ 零输入响应1.1零状态响应:lsim基于传递函数 H(s) 求解:视频:连续时间系统的时域分析1.2零输入响应:lsim基于状态空间模型求解:状态变量的初值容易求得


9、补充与扩展:逆矩阵问题1.如果想要CA矩阵可逆,可以先将 H(s) 里相同的零极点消除(注意:系统会因此而降阶),然后再转换成状态空间模型2.消除传递函数 H(s) 里相同的零极点,再转换成状态空间模型,可以保证CA矩阵可逆3.以上步骤,MATLAB里可以直接实现3.1sys = tf(num, den)3.2 sys_ss= ss(sys, 'minimal')3.3 状态空间模型sys_ss完全可观,完全可控3.4 特别注意:系统可能会降阶

