三者定义不同
(1)泰勒公式的定义为:若函数 f(x) 在包含x0的某个闭区间[a,b]上具有n阶导数,且在开区间(a,b)上具有( n+1)阶导数,则对闭区间[a,b]上任意一点x,有:
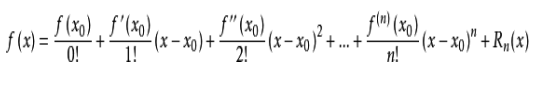
(2)Rn(X)是泰勒公式的余项,是 (x-x0)^n 的高阶无穷小。带拉格朗日余项的泰勒公式和带皮亚诺余项的泰勒公式是因余项不同而产生的泰勒公式的两种不同形式。
带拉格朗日余项的泰勒公式:余项 Rn(x) =[ f^(n+1) (ξ) *(x-x0)^(n+1) ] / (n+1)! ,ξ 介于x 、x0 之间;
带皮亚诺余项的泰勒公式:余项 Rn(x) = o[(x - x 0)^n] 。
(3)带拉格朗日余项的麦克劳林公式:麦克劳林公式是泰勒公式中的一种特殊形式,当x0 = 0 时,泰勒公式又称为麦克劳林公式。即:带拉格朗日余项的麦克劳林公式是带拉格朗日余项的泰勒公式在x0 = 0 时的形式。
2. 意义不同
(1)泰勒公式的意义是把复杂的函数简单化,即化成多项式函数,泰勒公式是在任何点的展开形式。
(2)麦克劳林公式的意义是在0点,对函数进行泰勒展开。
扩展资料:
其他形式的泰勒公式余项:
施勒米尔希-罗什余项: Rn(x)= f^(n+1)[x0+θ(x-x0)]*(1-θ)^(n+1-p)*(x-x0)^(n+1)/n!p θ∈(0,1)
柯西余项:Rn(x)= f^(n+1)[x0 +θ(x-x0)]*(1-θ)^n *(x-x0)^(n+1)/n!p θ∈(0,1)