1、读取数据集。sz_data=read.csv("sz_data.csv",head=T,encoding="utf-8")head(sz_data);dim(sz_data) #查看数据的前几行和数据维度

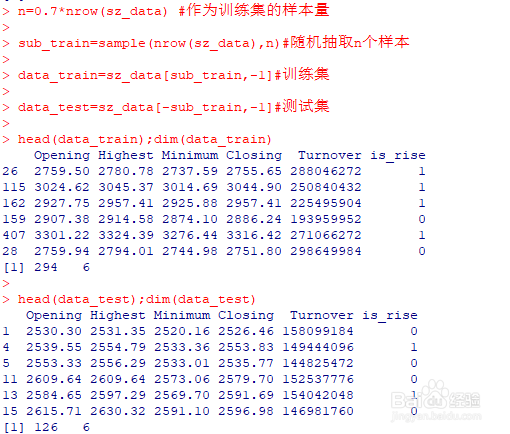
2、进行数据预处理。在实际应用中,如果数据有缺失值,需要先按照一定的方法先对缺失值进行处理。这里我们直接划分训练集和测试集,并且随机抽取70%的样本作为训练集。n=0.7*nrow(sz_data) #作为训练集的样本量sub_train=sample(nrow(sz_data),n)#随机抽取n个样本data_train=sz_data[sub_train,-1]#训练集data_test=sz_data[-sub_train,-1]#测试集head(data_train);dim(data_train)head(data_test);dim(data_test)
3、进行朴素贝叶斯判别分析,拉悟有仍该判别假设变量间是相互独立的。library(klaR)#加载软件包data_tra足毂忍珩in$is_rise=as.factor(data_train$is_rise) #数据格式转换为分类数据fit_Bayes1=NaiveBayes(is_rise~.,data_train) #建立判别公式names(fit_Bayes1)fit_Bayes1$apriori #先验概率fit_Bayes1$tables #所有变量条件概率plot(fit_Bayes1)#各类别下变量密度可视化从图中可以看出很多信息,比如对于0和1这两个类别,Minimum变量的分布差异并不明显。


4、对测试集所属类别进行预测。pre_Bayes1=predict(fit_Bayes1,data_test)data_test$Bayes_pre_rise=pre_Bayes1$class #输出类别预测结果head(data_test) #查看含有预测结果的数据

5、验证模型准确性。table(data_test$is_rise,pre_Bayes1$class) #生成is_rise的预测值和实际值的混淆矩阵error_Bayes1=sum(pre_Bayes1$class!=data_test$is_rise)/nrow(data_test);error_Bayes1#计算错误率混淆矩阵中,对角线上的数据是被准确判别了的。计算出的错误率超过了50%,效果不理想,可能是变量间并不相互独立造成的。实际应用中,可以先对数据集进行相关性检验,如果变量间相互独立,再采取朴素贝叶斯判别方法。
