1、第一,利用MATLAB优化工具箱提供的fminbnd,求下图函数f(x)=sin(x)+x*cos(x)在区间[0, 5]上的极大值与极小值。

2、第二,启动MATLAB,新建脚本(Ctrl+N),在脚本编辑区输入如下代码:
close all; clear all; clc
syms x
f=@(x) sin(x)+x*cos(x);
[xmin]=fminbnd(f,0,5),
[fxmin]=double(subs(f,x,[xmin]))
[xmax]=fminbnd(inline(-f(x)),0,5)
[fxmax]=double(subs(f,x,[xmax]))
ezplot(f,[0,5]);hold on
plot([xmin,xmax],subs(f,x,[xmin,xmax]),'ro','LineWidth',5)
text(xmin,double(subs(f,x,xmin)+0.2),'极小值')
text(xmax,double(subs(f,x,xmax)+0.2),'极大值'良矿)
其中f=@(x)是通过匿名函数的方法定义函数,inline( )是通过内联函数的方法定义函数,见百度经验《MATLAB学习与使用:定义函数(3种方法)》,《
MATLAB学习与使用:内联函数(inline)及其应用》。subs( )是置换函数,即求x取[xmin]或者[xmax]时,函数f的值。
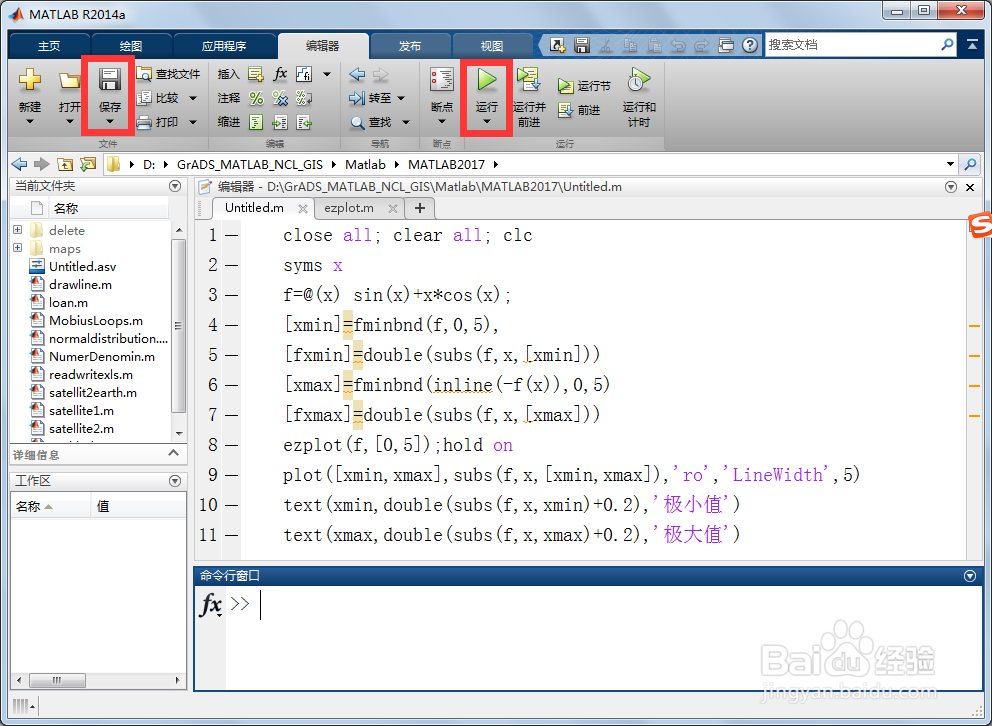
3、第三,保存和运行上述脚本,在命令行窗口返回如下结果:
xmin =
3.6436
fxmin =
-3.6752
xmax =
1.0769
fxmax =
1.3910
也就是说,函数f(x)=sin(x)+x*cos(x)在区间帽巨[0, 5]上的极小值为 -3.6752,极大值为1.3910,分别位于在x=3.6436和x=1.0769处。

4、第四,保存和运行上述脚本也会得到以下图像,我们可以看到函数f(x)=sin(x)+x*cos(x)的曲线,以及它在区间[0, 5]上的极大值与极小值。

5、第五,关于fminbnd的详细介绍,可国婶艳以在命令行窗口输入doc fminbnd,查看MATLAB帮助文档对它的介绍。
