1、首先,给出s4的矩阵表示。
这是24个置换矩阵。

2、第一个矩阵是二阶矩阵{{0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}}:
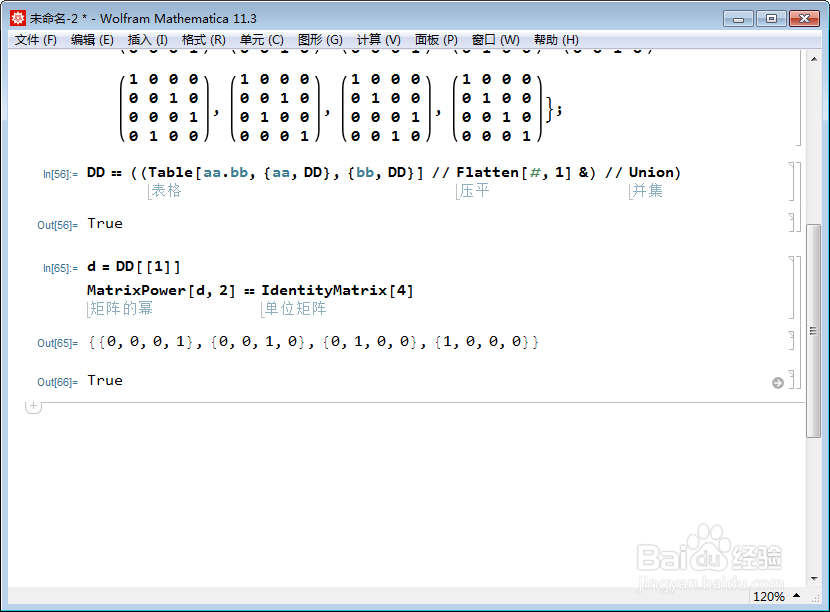
d = DD[[1]]
MatrixPower[d, 2] == IdentityMatrix[4]
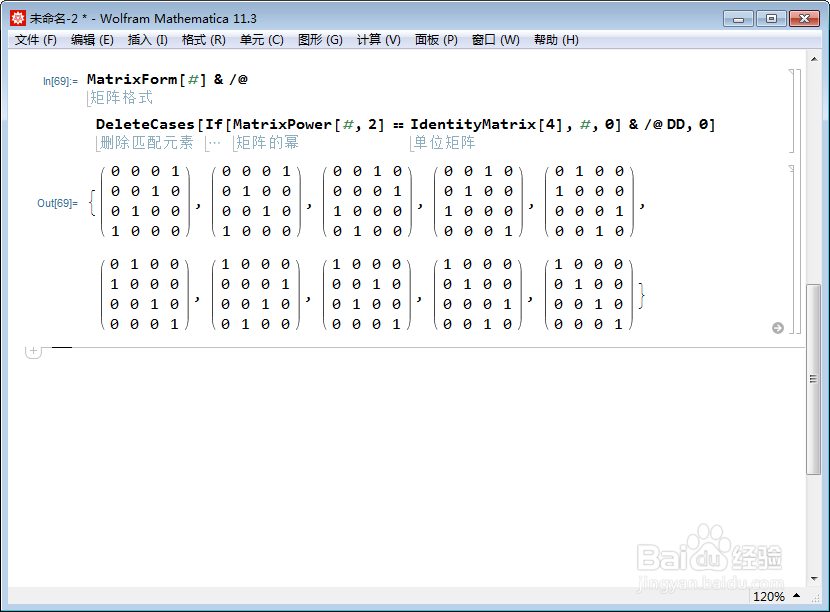
3、用这个方法,可以搜索出所有的二阶元素:
MatrixForm[#] & /@
DeleteCases[If[MatrixPower[#, 2] == IdentityMatrix[4], #, 0] & /@ DD,0]
一共有10个二阶元素?
不,需要抛去单位元。
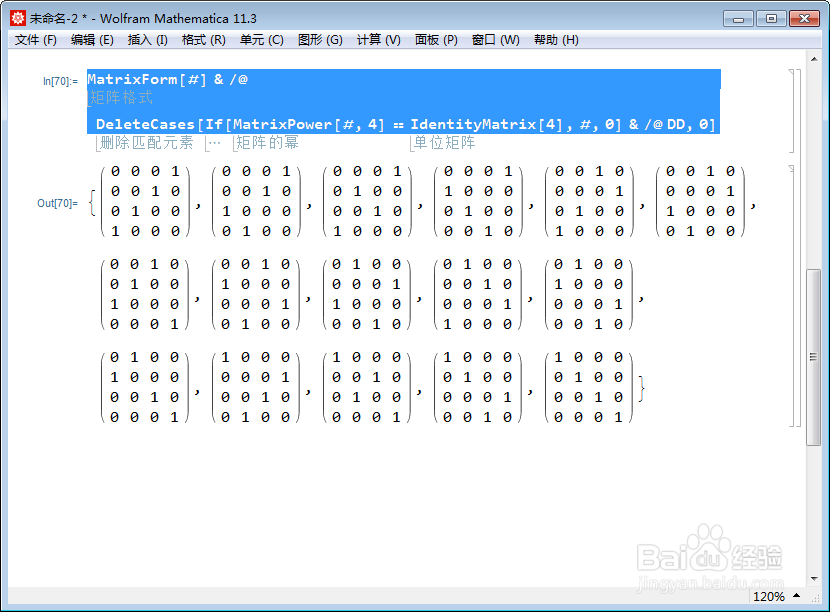
4、4阶元素有多少个?
MatrixForm[#]&/@DeleteCases[If[MatrixPower[#,4]==IdentityMatrix[4],#,0]&/@DD,0]
这个方法,得到16个,但,这是错的。因为把二阶元素也算进去了。
5、可以这样寻找4阶元素,一共有6个。

6、3阶元素有8个:

7、没有6阶、8阶、12阶元素?

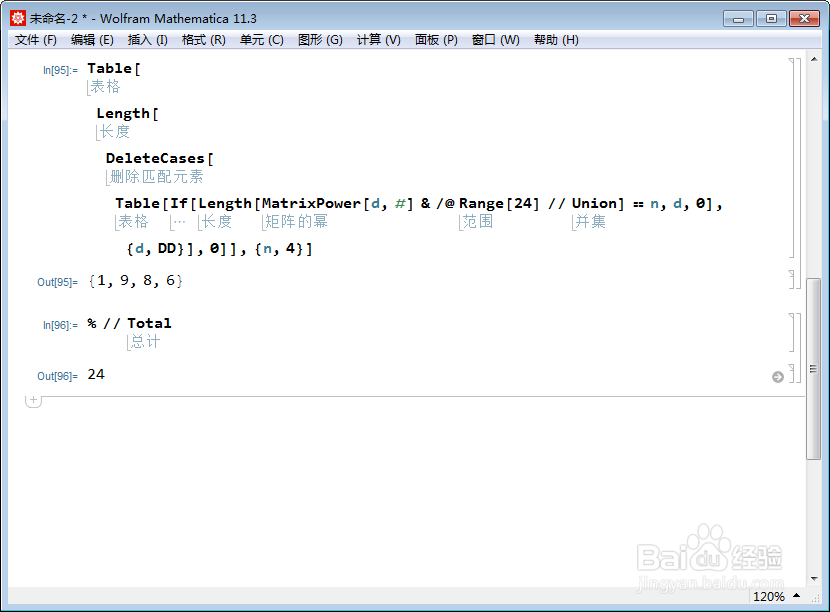
8、一阶、二阶、三阶、四阶元素的个数,分别是1、9、8、6,其和恰好等于24。