1、※.函数的定义域根据函数特征,对lnx有x>0,对√2x有x≥0,则x>0,即函数的定义域为:(0,+∞)。
2、※.函数的单调性根据函数的单调性,函数y1=lnx在定义域上为增函数,函数y2=√2x在定义域上为增函数,则和函数y=y1+y2也为增函数。函数还可以用导数来解析单调性,步骤如下:∵y=lnx+√2x∴dy/dx=1/x+1/(2√2x)又因为x>0,则:1/x>0,1/(2√2x)>0,即dy/dx>0,函数y在定义域上为单调增函数。
3、※.函数的凸凹性∵dy/dx=1/x+1/(2√2x)=1/x+x^(-1/2)/(2√2)∴d^2y/dx^2=-1/x^2-x^(-3/2)/(4√2)=-[1/x^2+x^(-3/2)/(4√2)]<0,即函数在定义域上为凸函数。
4、※.函数的极限lim(x→0) lnx+√2x=-∞;lim(x→+∞) lnx+√2x=+∞。
5、函数的五点图:
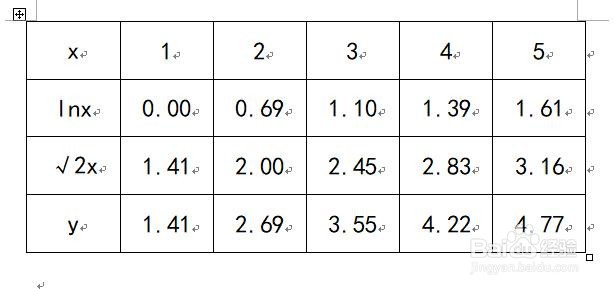
6、函数的示意图:
