1、方阵 A 的特征值和特征向量分别为满足以下条件的标量 λ 和非零向量 υ
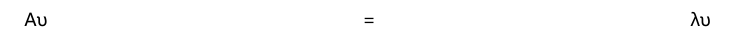
2、对于对角矩阵的对角线上的特征值 Λ 以及构成矩阵列的对应特征向量 V，公式为
3、如果 V 是非奇异的，这将变为特征值分解。
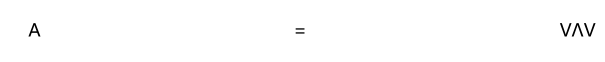
4、微分方程 dx/dt = Ax 的系数矩阵就是一个很好的示例：
5、此方程的解用矩阵指数 x(t) = e tA x(0) 表示。语句lambda = eig(A)生成包含 A 的特征值的列向量。对于该矩阵，这些特征值为复数：
6、每个特征值的实部都为负数，因此随着 t 的增加，e λt 将会接近零。两个特征值 ±ω 的非零虚憧钏荭拜部为微分方程的解提供了振动分量 sin(ωt)。使用这两个输出参数，eig 便可以计算特征向量并将特征值存储在对角矩阵中：[V,D] = eig(A)
7、第一个特征向量为实数，另外两个向量互为共轭复数。所有三个向量都归一化为具有等于 1 的欧几氇筐塘瓠里德长度 norm(v,2)。矩阵 V*D*inv(V)（可更简脱噱癌敷洁地写为 V*D/V）位于 A 的舍入误差界限内。inv(V)*A*V 或 V\A*V 都在D 的舍入误差界限内。