1、 y=x-(x-1)^(-1),含有分式函数,则x-1≠0,即x≠-1.
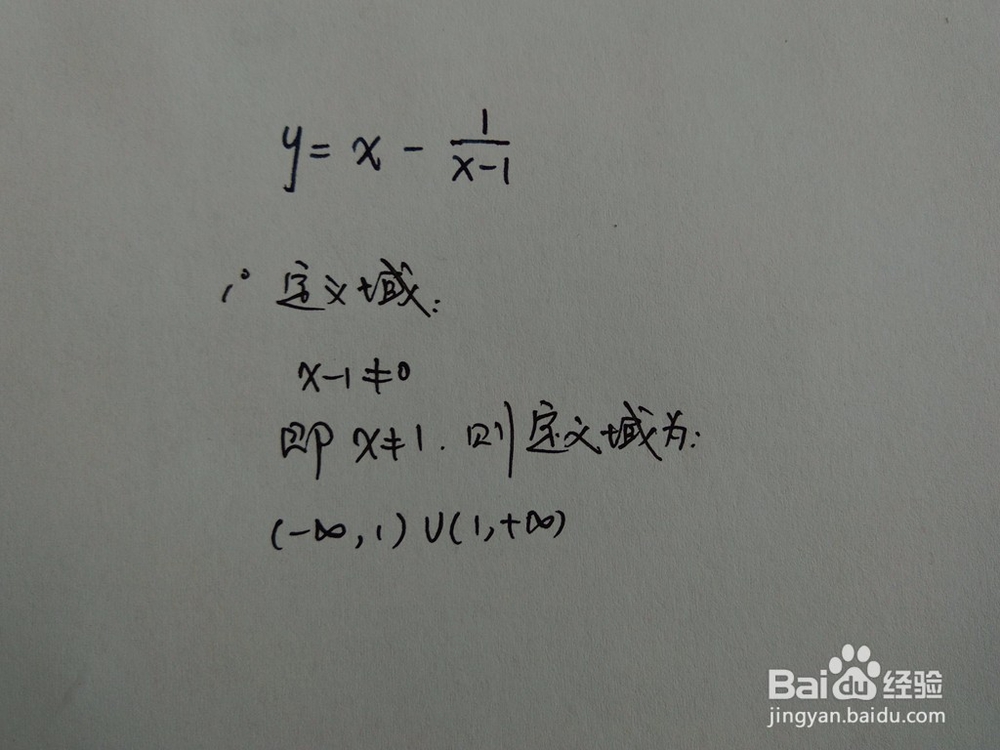
1、 利用函数的导数知识,通过函数的一阶导数,判断函数y=x-(x-1)^(-1)的单调性,并求出函数的单调区间。

1、 利用函数的导数知识,通过函数的二阶导数,判断函数y=x-(x-1)^(-1)的凸凹,并求出函数的凸凹区间。

1、 本步骤介绍函数 y=x-(x-1)^(-1) 在x趋近于无穷大及x趋近于1时的极限。

1、 函数 y=x-(x-1)^(-1) 的五点图如下图:
2
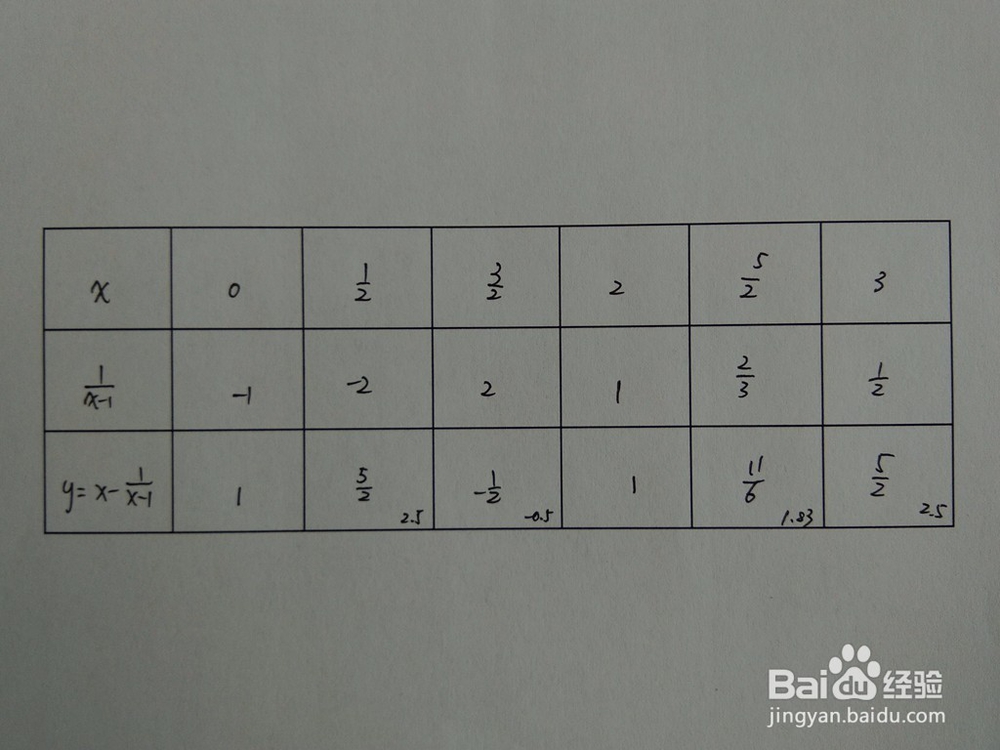
3

1、 函数y=x-(x-1)^(-1)在二维坐标系下的示意图。
