具体回答如图:
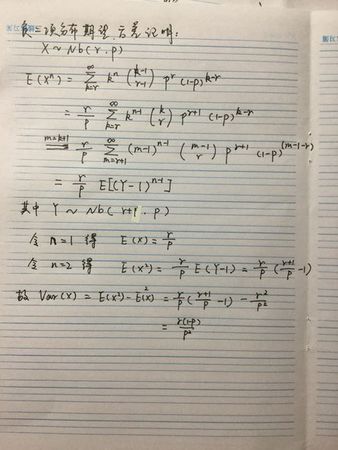
负二项分布是统计学上一种离散概率分布。满足以下条件的称为负二项分布:实验包含一系列独立的实验, 每个实验都有成功、失败两种结果,成功的概率是恒定的,实验持续到r次成功,r为正整数。
扩展资料:
已知一个事件在伯努利试验中每次的出现概率是p,在一连串伯努利试验中,一件事件刚好在第r + k次试验出现第r次的概率。
满足以下条件的称为负二项分布:
1、实验包含一系列独立的实验。
2、每个实验都有成功、失败两种结果。
3、成功的概率是恒定的。
4、实验持续到r次成功,r可以为任意正数。
假设有一组独立的伯努利数列,每次实验有两种结果“成功”和“失败”。每次实验的成功概率是p,失败的概率是1-p。我们得到一组数列,当预定的“非成功”次数达到r次,那么结果为“成功”的随机次数会服从负二项分布。
P表示失败的概率,不是成功的。为了把公式进行转换,每个地方用1-p代替p。X定义为失败次数,而不是成功的,这里的定义X为失败的,但P是成功的,和前面X表示成功但P表示失败概率的情况用同样的公式。但是失败和成功的描述是一致的,并且和前面的进行替换。
参考资料来源:百度百科——负二项分布