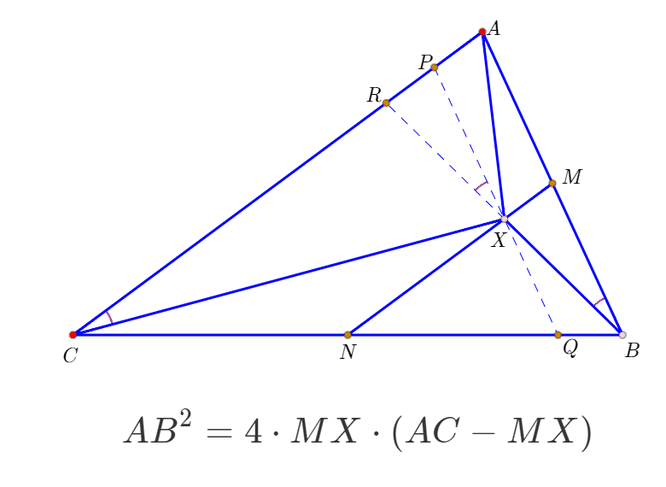
1、设BX的延长线交AC于R,那么X就是BR的中点,AR=2MX。

2、过X作AB的平行线,交AC、BC于P、Q,那么,P是AR中点。

3、注意角度相等的关系,可以得出结论:PX^2=PR*PC。

4、注意到PX=AB/2,PC=AC-AP=AC-PR=AC-MX,所以得到如下关系:
AB^2=4*MX*(AC-MX)
5、解这个关于MX的方程,得到两个解:

6、这两个解有一个大于AC/2,不符合题意,只能保留较小的那个解。
由此可以求出NX的大小:
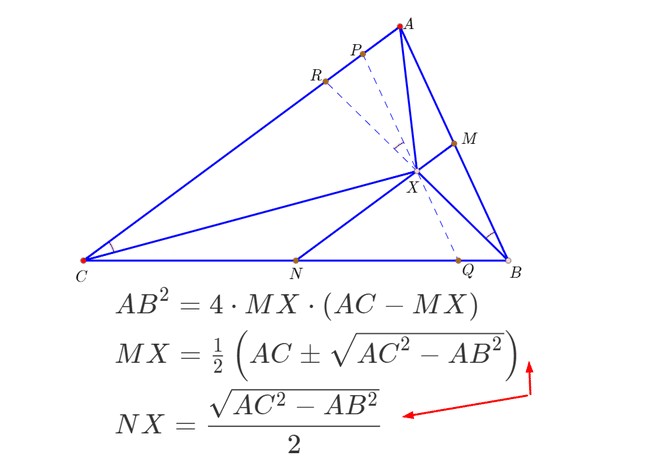
7、注意到AC>AB,所以点X始终位于MN之间。
以N为圆心、sqrt(AC^2-AB^2)/2为半径作圆,与线段MN的交点,即为X点。
