典型的指派问题(assignment problem):有若干项任务,每项任务必须有一人且只能有一人承担,每人也只能承担其中一项,不同人员承担不同任务的收益(或成本)不同,问题是怎样分派各项任务使总收益最大(或总成本最小). 由于每个工人必须做且只能做一项工作,第i 个工人是否做第j 个工作可以用0-1 型变量表示. 所以这类问题建立的数学模型是0-1型整数规划.指派问题是很常见的一类问题,很容易建立对应的0-1 规划模型. 这类模型通常规模会很大. 例如给100 个人指派100 项工作,模型具有10000 个决策变量. 使用LINGO求解时,有大量的数据需要输入、输出. 可以利用Excel 作为工具解决数据输入输出问题.
工具/原料
Lingo 17 X64位商业版
Windows 10家庭中文版
实例
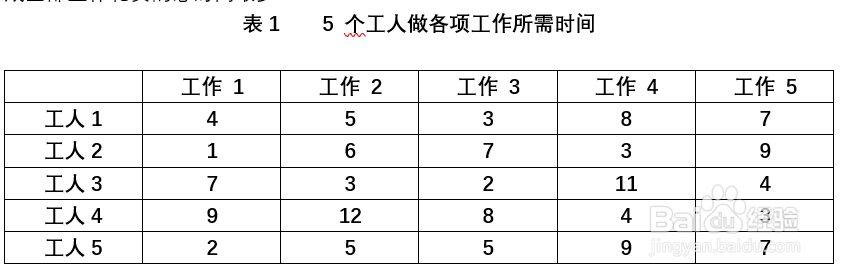
1、工作分配问题 :5 个工人的车间接到5 项不同的工作. 每个工人做每项工作熟练程度不同,所以完成所需时间不同(见表2.6). 每个工人必须做且只能做一项工作. 如何分配工作才能使完成全部工作花费的总时间最少?
2、模型建立:

3、模型榨施氅汝求解用LINGO 17求解. 输入代码如下:model:sets:workers/w1..w5/;jobs/j1..j5/;links(workers,jobs):cost,x;endsetsmin=@sum(links:cost*x);@for(workers(i):@sum(jobs(j):x(i,j))=1;);@for(jobs(j):@sum(workers(i):x(i,j))=1;);@for(links:@bin(x));data:cost=4 5 3 8 71 6 7 3 97 3 2 11 49 12 8 4 32 5 5 9 7;enddataend
4、注意 这里用到了LINGO 17 的两个循环函数:@for( )和@sum( ). 循环变量需要通过集的名称来设定,集可以是二维或更高维的. 例如,@for(links:@bin(x))可以设定二维变量x(i,j)全部为0-1 型变量.求解的结果如下:


5、结果显示:工人1 做工作3,工人2 做工作4,工人3 做工作2,工人4 做工作5,工人5 做工作1,花费的总时间最少为14,其中14=3+3+3+3+2.