1、一,万事开头难,以公式为例;1,公式的内容;2,公式的条件;3,公式的结果;4,公式的影响;5,公式的基本概念;6,公式的模型;7,公式的证明;举个例子:勾股定理;

2、公式内容:直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方;也就是说,设直角三角形两直角边为a和b,斜边为c,那么a²+b²=c²


3、公式条件:直角;
4、公式结果:两直角边边长平方和等于斜边边长的平方;
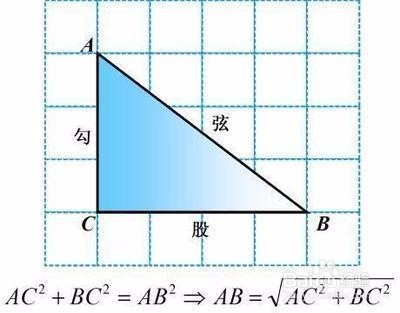
5、公式的影响:知道了两条直角边的长度,即可推算出斜边的长度;
6、公式的基本概念:直角边,斜边,直角;不懂的要查清楚这些概念是什么意思,例如什么是斜边等等;
7、公式的模型:有一个直角三角形,确定了两条边,也等于确定了斜边;

8、公式的证明:先不看书,自己洵翌绦枞证明一下,不懂的再参考;勾股定理-欧几里德证明法:证明的思路为:从A点划一直线至对边,使其垂直于对边。延长此线把对边上的正方形一分为二,把上方的两个正方形,通过等高同底的三角形,以其面积关系,转换成下方两个同等面积的长方形。设△ABC为一直角三角形,其直角为∠CAB。其边为BC、AB和CA,依序绘成四方形CBDE、BAGF和ACIH。画出过点A之BD、CE的平行线,分别垂直BC和DE于K、L。分别连接CF、AD,形成△BCF、△BDA。∠CAB和∠BAG都是直角,因此C、A和G共线,同理可证B、A和H共线。∠CBD和∠FBA都是直角,所以∠ABD=∠FBC。因为AB=FB,BD=BC,所以△ABD≌△FBC。因为A与K和L在同一直线上,所以四边形BDLK=2△ABD。因为C、A和G在同一直线上,所以正方形BAGF=2△FBC。因此四边形BDLK=BAGF=AB²。同理可证,四边形CKLE=ACIH=AC²。把这两个结果相加,AB²+AC²=BD×BK+KL×KC由于BD=KL,BD×BK+KL×KC=BD(BK+KC)=BD×BC由于CBDE是个正方形,因此AB²+AC²=BC²,即a²+b²=c²。

9、在公式的学习方法中,可以领悟到,在数学的整个学习过程中,就是要不断锻炼自己的动脑能力,多问为什么;老师不能把他懂的知识搬到你脑里,只有自己不断的思考,总结经验,才能不断提升数学思维;