1、pi分形目前难以用网络画板画出来，因为网络画板关于pi的精度，只能达到小数点后面20位。
2、考察一个特殊数列，这个数列要求网络画板给出前3000项。1,2,2,3,补朱锚卦3,3,4,4,4,4,5,5,5,5,5,……这个数列的规律是，1个1，2个2，3个3，4个4，5个5，6个6，……依次排列而成。
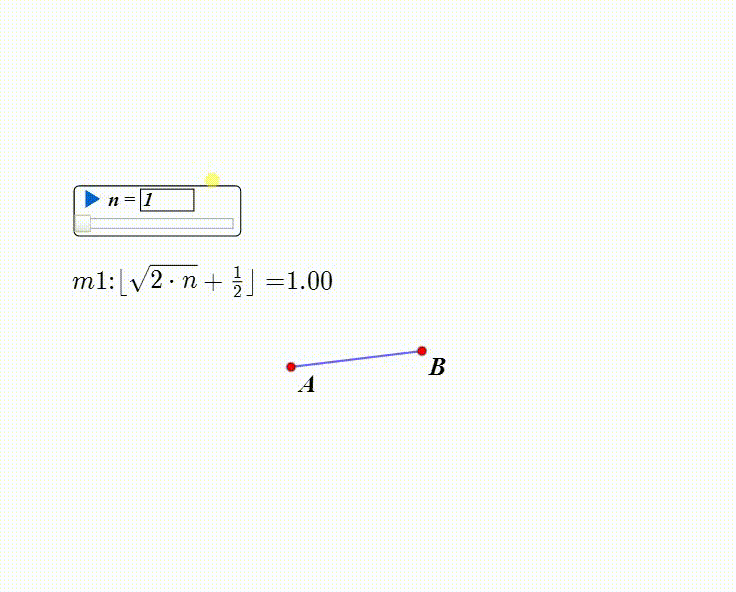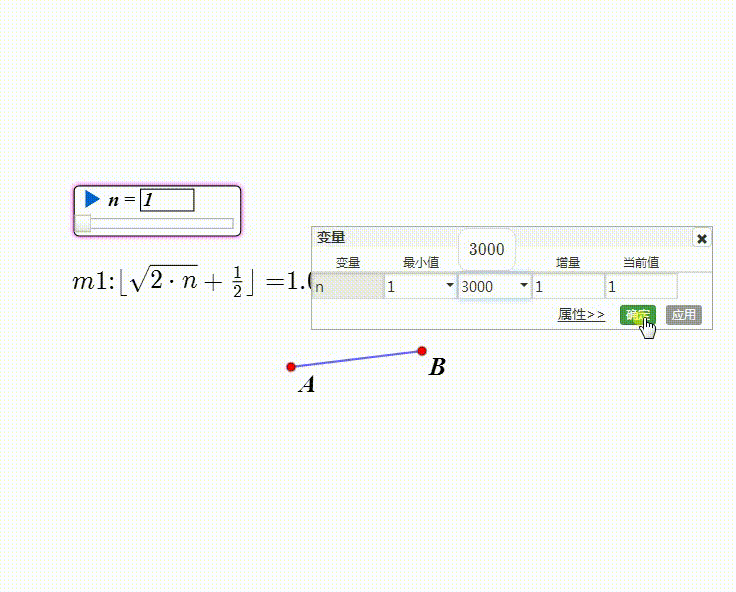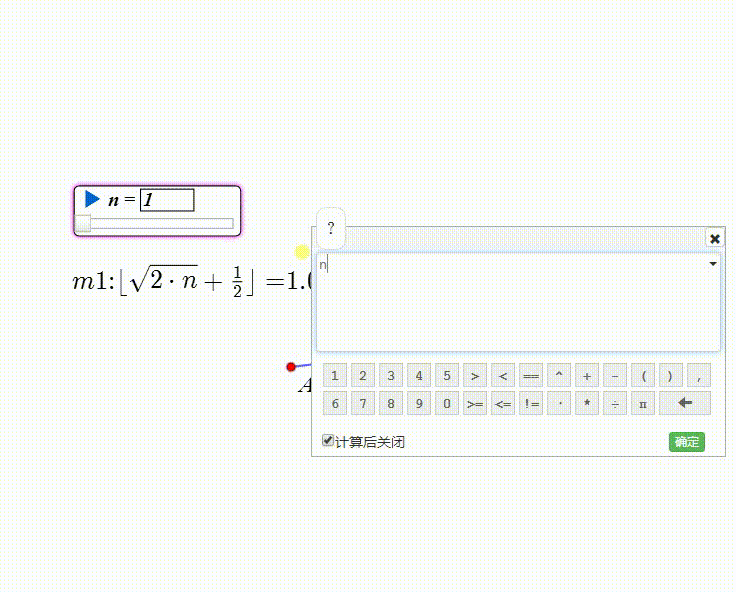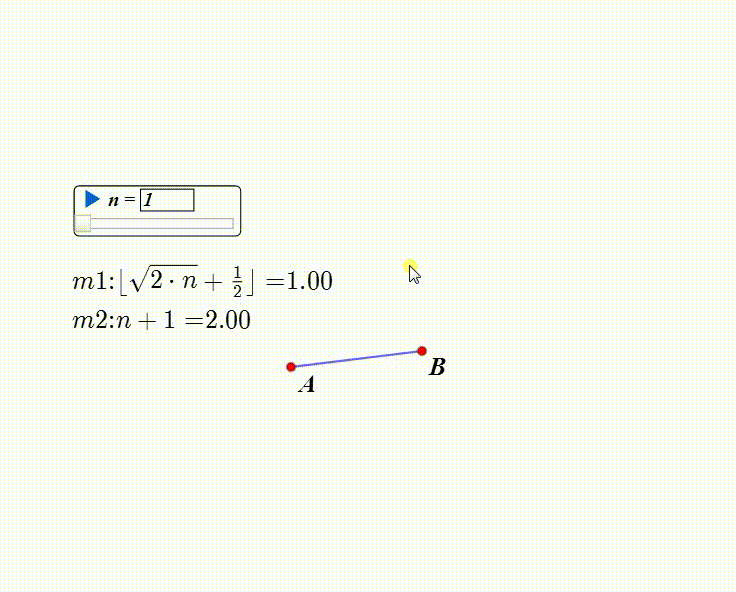
3、这个数列的通项公式可以写为：floor(sqrt(2*n) + 1 / 2)
4、绘制线段AB。
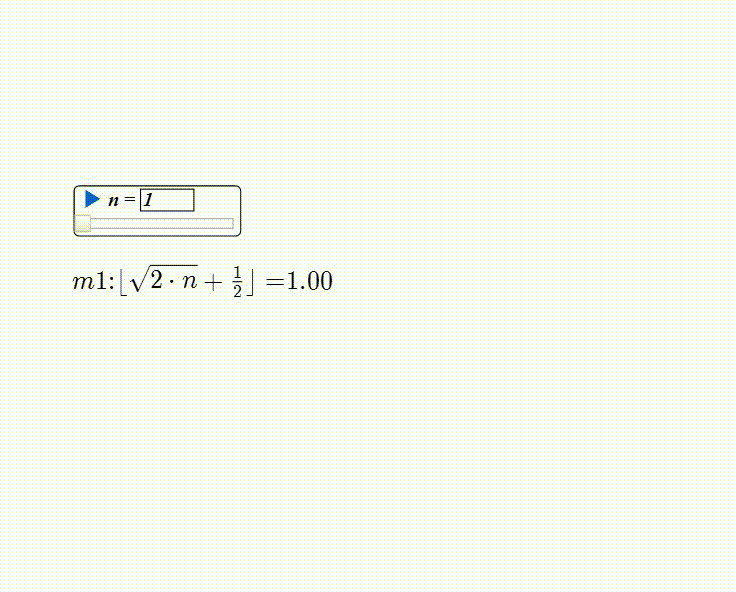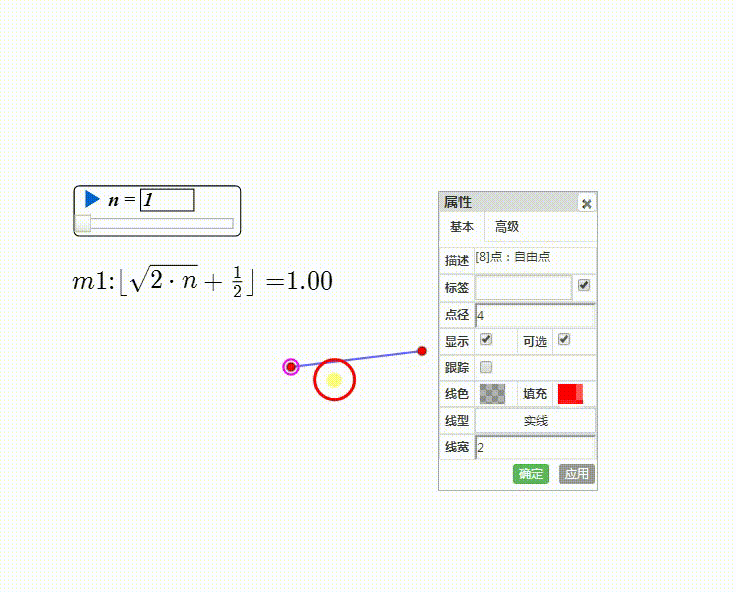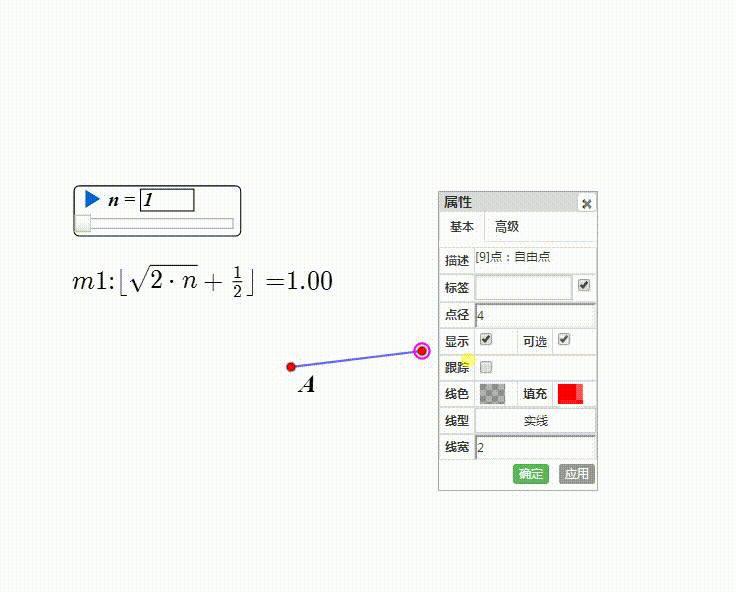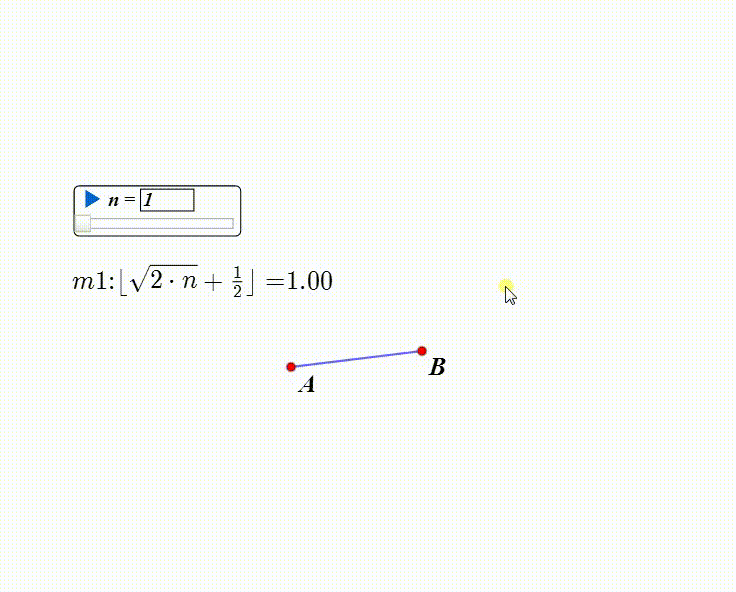
5、构造变量n，最小值为1。计算m2=n+1。
6、A绕B，逆时针旋转((-1)^(floor(sqrt(2*n) + 1 / 2)))*pi/2的弧度，得到点C。
7、选择A、B和变量n，进行迭代变换：A→BB→Cn→m2只保留非点类迭代，迭代深度为m。
8、构造变量m，最小值为0，最大值为3000，增量为1。
9、缩小AB距离，改变AB位置，看看m逐步增大的动画效果。发现蚂蚁被局限在一个有限区域内活动。
10、采用别的数列通式和旋转角度试一下。但是，数列的每一项都必须是正整数，否则(-1)^an容易出错；因滠锖斟绸此，采用floor函数取整。((-1) ^ (floor(sin(sqrt(2* n) + 1 / 2)))) * 2 * pi / 3
11、如果旋转角度改为：((-1) ^ (f盟敢势袂loor(cos(sqrt(2 n) + 1 / 2)))) * 3 * pi / 5效果如下。
12、((-1) ^ (floor(cot(sqrt(2 n) + 1 / 2)))) * pi / 5
