介绍使用Mathematica计算数论中的乘法阶数。这一阶数的计算是原根/指数理论的基础,和一些同余方程的求解密切相关。
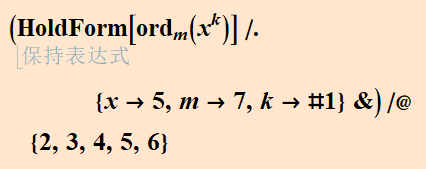
工具/原料
Mathematica
方法/步骤
首先,在Mathematica中我们可以直接使用FindInstance求出同余方程特解,或者使用Reduce尝试求通解。
其中形如X^n≡c(mod m),c与m互素的这一类方程,其背后的原理是求出x^n≡c(mod m)的一个特解,然后求出y^n≡1(mod m)的通解,相乘即得到原方程全部解。

而阶数的数学定义如图所示。注意a和m要互素。互素时A集合一定非空。
阶数一定存在。

在Mathematica中,可以使用PowerMod[x,n,m]代替Mod[x^n,m],它们含义相同,但是幂模的计算可以比模余优化一些。

如图是手算阶数的过程。
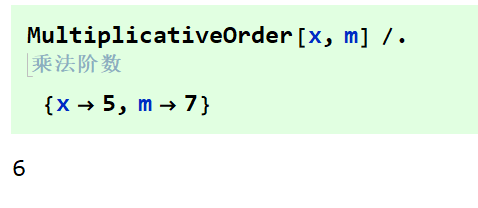
依次计算幂模,带入n为1~9,发现当n=6时,幂模是1.
也就是说x模m(5模7)的阶数是6.

如图是使用Mathematica的乘法阶数函数MultiplicativeOrder直接计算阶数的过程。
如果a与m互素,那么a^k与m同样互素。
要计算a^k模m的乘法阶数,首先我们可以使用Mathematica暴力求解如图。

我们也可以根据推导得出a^k模m的阶数为L/GCD[L,k],其中L是a模m的阶数。
带入比较,与暴力解法所得阶数相同。

注意事项
MultiplicativeOrder还可以用于计算广义乘法阶数。