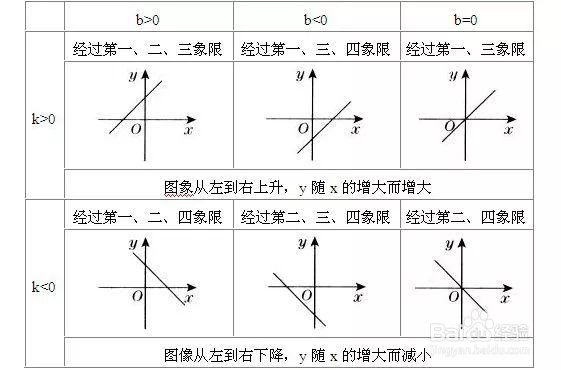
1、一鸱远忡绑次函数的性质。正比例函数y=kx+b有下列性质:1.y的变化值与对应的x的变化值成正比例,比值为k。即:y=kx+b(k≠0)(k不等于0,且k,b为常数)。2.当x=0时,b为函数在y轴上的交点,坐标为(0,b)。 当y=0时,该函数图像在x轴上的交点坐标为(-b/k,0)。3.k为一次函数y=kx+b的斜率,k=tanθ(角θ为一次函数图像与x轴正方向夹角,θ≠90°)。4、当b=0时(即y=kx),一次函数图像变为正比例函数,正比例函数是特殊的一次函数。5、函数图像性质: 当k相同,且b不相等,图像平行; 当k不同,且b相等,图像相交于Y轴; 当k互为负倒数时,两直线垂直。6、平移时:上加下减在末尾,左加右减在中间。
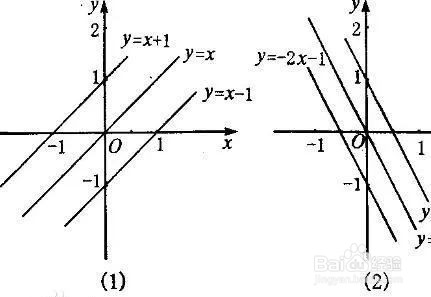
2、正比例函数的对称性当平面直角坐标系中两直线平行时,其函数解析式中k的值(即一次项系数)相等;当平面直角坐标系中两直线垂直时,其一次函数斜率的乘积=-1。
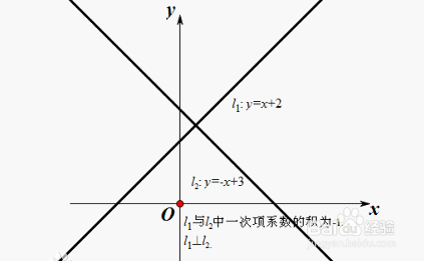
3、一次函数的表示法一次函数有三种表示方法,如下:1、解析式法用含自变量x的式子表示函数的方法叫作解析式法。2、列表法把一系列x的值对应的函数值y列成一个表来表示的函数关系的方法叫作列表法。3、图像法用图像来表示函数关系的方法叫作图像法。

4、函数图像的性质1.在一次函数上的任意一点P(x,y),都满足等式:y=kx+b(k≠0)。2.一次函数与y轴交点的坐标缍那傺蒙总是(0,b),与x轴总是交于(-b/k,,0)。正比例函数的图像都是过原点。3、函数不是数,它是指某一变化过程中两个变量之间的关系。4、k,b与函数图像所在象限:y=kx时(即b等于0,y与x成正比,此时的图像是一条经过原点的直线)当k>0时,直线必通过一、三象限,y随x的增大而增大;当k<0时,直线必通过二、四象限,y随x的增大而减小。y=kx+b(k,b为常数,k≠0)时:当k>0,b>0,这时此函数的图像经过一,二,三象限;当k>0,b<0,这时此函数的图像经过一,三,四象限;当k<0,b>0,这时此函数的图像经过一,二,四象限;当k<0,b<0,这时此函数的图像经过二,三,四象限。当b>0时,直线必通过一、二象限;当b<0时,直线必通过三、四象限。特别得,当b=0时,直线通过原点O(0,0)表示的是正比例函数的图像。当k>0时,直线只通过一、三象限,不会通过二、四象限。当k<0时,直线只通过二、四象限,不会通过一、三象限。5、特殊位置关系当平面直角坐标系中两直线平行时,其函数解析式中K值(即一次项系数)相等。当平面直角坐标系中两直线垂直时,其函数解析式中K值的乘积为-1。6、直线y=kx+b的图像和性质与k、b的关系如下表所示:k>0,b>0:经过第一、二、三象限k>0,b<0:经过第一、三、四象限k>0,b=0:经过第一、三象限(经过原点)结论:k>0时,图像从左到右上升,y随x的增大而增大。k<0,b>0:经过第一、二、四象限k<0,b<0:经过第二、三、四象限k<0,b=0:经过第二、四象限(经过原点)结论:k<0时,图像从左到右下降,y随x的增大而减小。7、将函数向上平移n格,函数解析式为y=kx+b+n,将函数向下平移n格,函数解析式为y=kx+b-n,将函数向左平移n格,函数解析式为y=k(x+n)+b,将函数向右平移n格,函数解析式为y=k(x-n)+b。