1、水面上的波小絮扬片纹,大体上是逐步衰减的正弦波动,因此可以用如下的参数方程,来表示某一刻的波动:{x, y, Sin[0.02 ((x + 10)^2 + y^2) ] + 0.9^((x + 10)^2 + y^2)}

2、加上一个时间参数n,就可以视为动画:{x, y, Sin[0.02 ((x + 10)^2 + y^2) - n] + 0.9^((x + 10)^2 + y^2)}
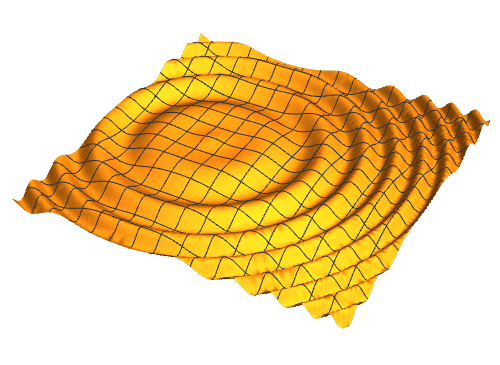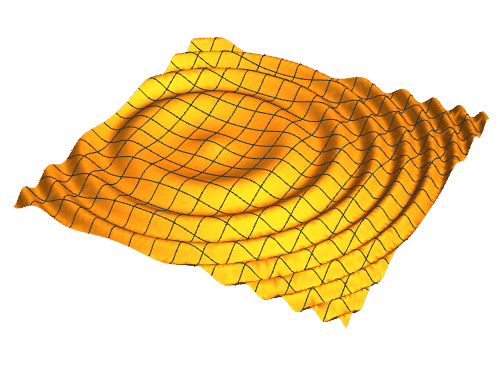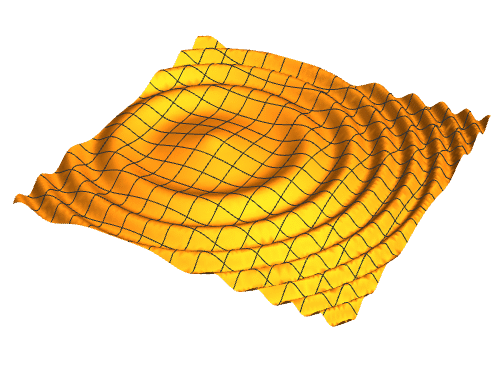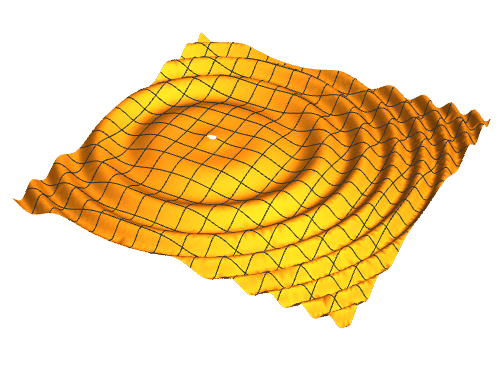
3、加快一下速度,就是要把"DisplayDurations" -> 0.1的时间缩短一下:"DisplayDurations" -> 0.02

4、上面波纹的中心点的坐标是(-10,0)。如果在(10,0)点的位置上,再出现一个波动,这两个波动会如何叠加?简单的加法就可以实现:Sin[0.03 ((x + 10)^2 + (y + 0)^2) - n] + 0.9^((x + 10)^2 + (y + 0)^2)+ Sin[0.03 ((x - 10)^2 + (y + 0)^2) - n] + 0.9^((x - 10)^2 + (y + 0)^2)

5、让两个波源离远点:Sin[0.03 ((x + 20)^2 + (y + 0)^2) - n] + 0.9^((x + 20)^2 + (y + 0)^2)+ S足毂忍珩in[0.03 ((x - 20)^2 + (y + 0)^2) - n] + 0.9^((x - 20)^2 + (y + 0)^2)

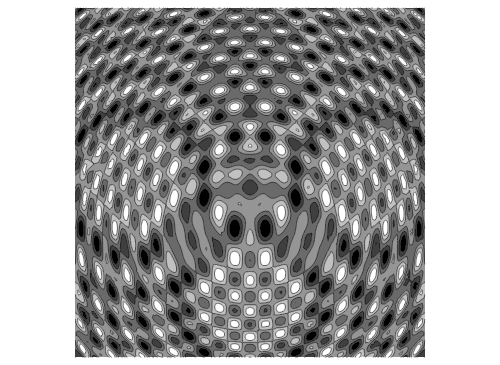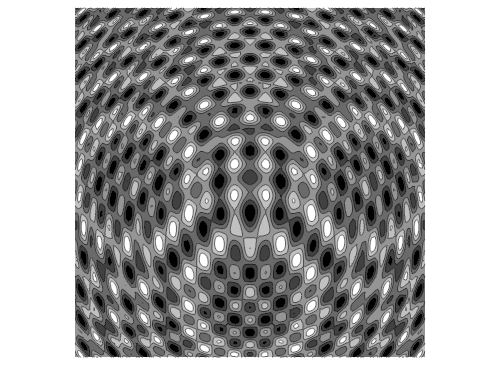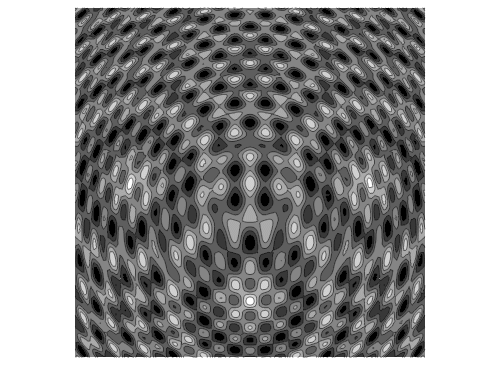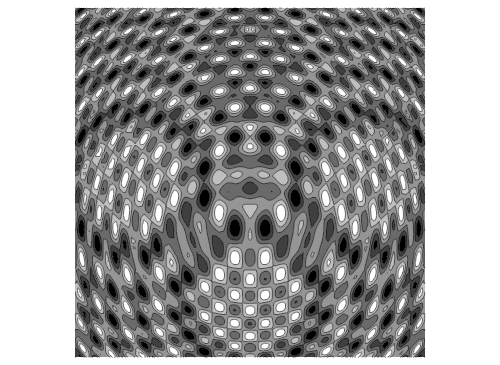
6、用contourPlot来绘制等高线图,看着会比较清晰:

7、如果再加上第三个波源:……+Sin[0.03 ((x + 0)^2 + (y + 20)^2) - n] + 0.9^((x - 0)^2 + (y + 20)^2)

8、三个波源的等高线图如下: