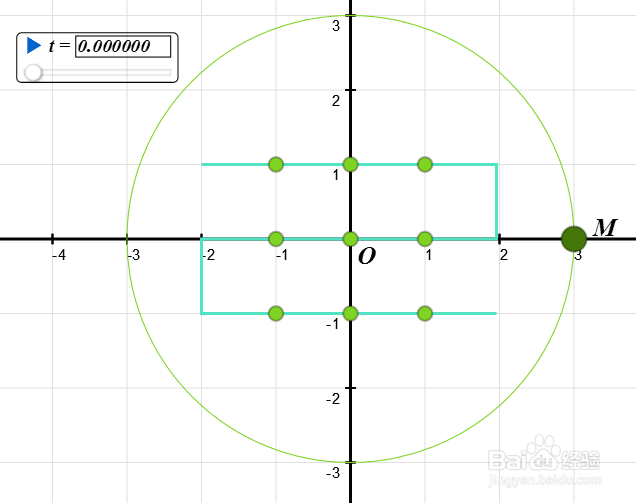
1、在平面上构造九个点,横坐标和纵坐标分别取值-1、0、1。

2、很明显,这九个点并不能确定一条三次曲线,还需要第10个点。
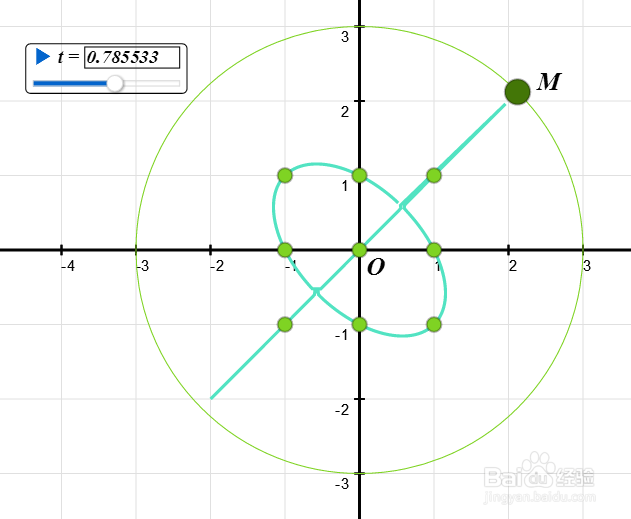
这第10个点,我们取半径为3的圆上的动点M,圆心位于原点。
过九点的任意三次曲线于这个圆必定有交点,
所以,这个动点M遍历整个圆周之后,三次曲线也遍历了所有情形。

3、根据十个点的坐标,可以求出三次曲线的隐函数方程:
[ (3cos(t)) ^ 3-3cos(t)] * (y ^ 3 - y)= [(3sin(t)) ^ 3-3sin(t)] * (x ^ 3 - x)
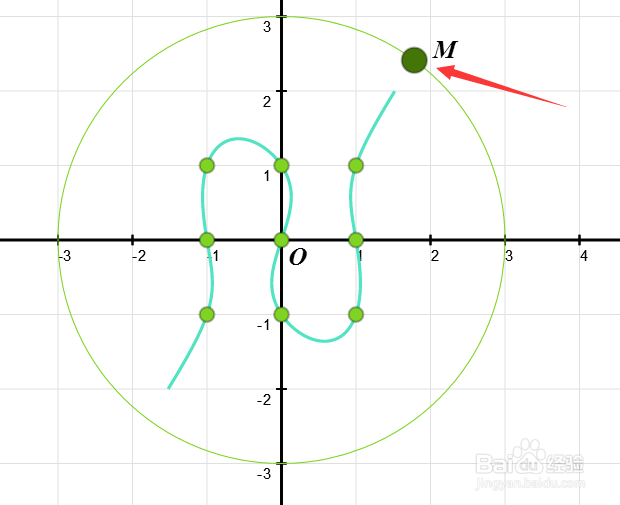
作出这个隐函数的图像。
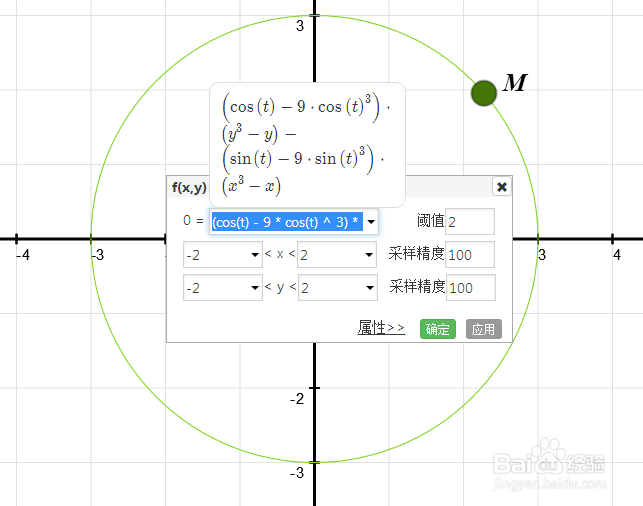
4、把M的属性里面的拖动值和点值都改为t。

5、这样,拖动M,可以改变三次曲线的形状。
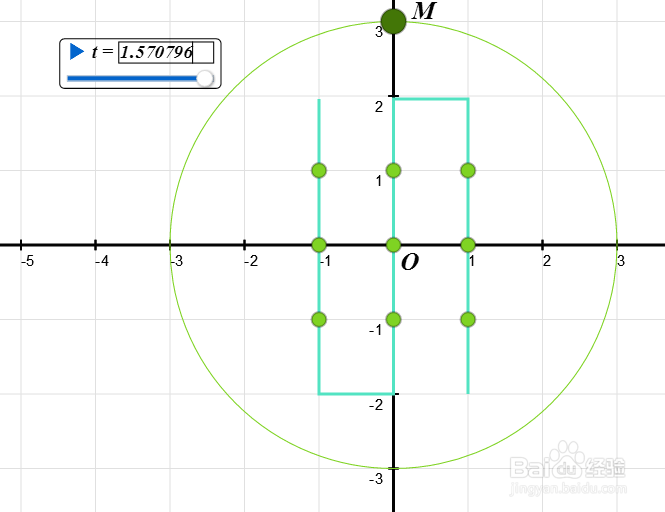
6、构造变量t。
当t=pi/4的时候,三次曲线退化为一个椭圆和一条直线。
7、当t等于pi/2的整数倍的时候,三次曲线退化为三条直线。