主对角线为0,其余为1的行列式值为(-1)^(n-1) * (n-1)。
只要将原行列式转化为上三角或下三角行列式即能求解,原行列式:

首先应当尽量多的消除1,因此将第二行到第n行均减去第一行,即令r2-r1,r3-r1,...,rn-r1,所得结果如下:

对于下三角部分,只要将第一列多余的1变换成0就可以形成上三角行列式,而此时恰好对角线均为-1,因此令第一列加上第二列、第三列直到第n列,即令c1+c2+...cn,得:

计算该行列式得结果为
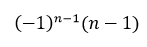
拓展一下
该行列式也可使用“加边法”来做,即将原行列式左边增加一列0,然后上面增加一行1,变为(n+1) * (n+1)的行列式,此行列式与原行列式等价。计算新行列式的值,从第二行起到第n+1行分别减去第一行,之后再令第一列加上第二列、第三列直到第n+1列,同样可得结果。