1、在似然比检验中,我们设参数空间为θ我们的原假设与备选假设为:
原假设:参数θ属于参数空间的θ的一个子集θ0
备选假设:参数θ属于θ0在参数空间的θ下的补集
如果用数学语言,可以表示为:

2、似然函数表示的是当前参数条件下,出现待估计数据的可能性大小,可以看做是x确定条件下的参数θ的一个函数,通常用x的概率密度函数或者概率质量函数来表示,数学公式表示为:

3、似然比检验需要使用两个模型的似然函数来构建统计量,其统计量公式可表示如下,其中sup表示集合的上确界:
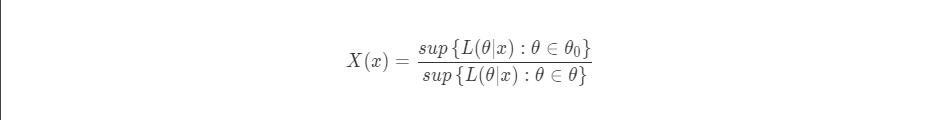
4、接下来,我们要确定的是该检验的拒绝域(reject region)或者关键值(critical value),常用的办法是,根据θ0和θ的参数个数差,来获得对应的卡方分布的分位数,卡方分布的自由度为参数个数差,分位数的比例为统计检验的置信度(通常为0.95),假设自由度为df,则对应的数值为:

5、接下来,我们就可以利用python来获得上述的关键值了,scipy这一包为我们提供了各类常用分布的各类函数,其中ppf函数为我们计算对应百分比的分位数,如果要是用卡方分布的功能,需要通过:
from scipy.stats import chi2
来引入chi2
然后使用:
chi2.ppf(q, df)
来获取对应的卡方分布分位数。
图示为自由度为21的卡方分布95%分位数:

6、接下来我们将-2log(X)来于对应的关键值c(刚才获得的分位数)进行比较,如果-2log(X)大于关键值c,则不拒绝原假设,反之拒绝原假设。