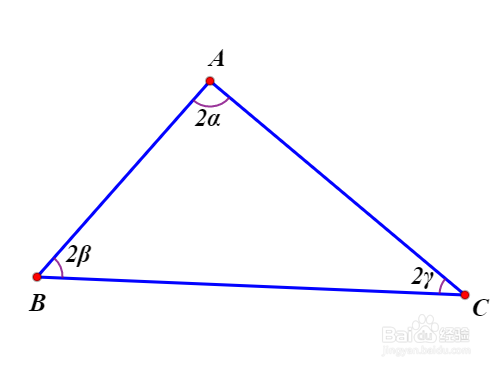
1、先介绍一个引理:设△ABC的三个内角是A=2α、B屏顿幂垂=2β、C=2γ,△ABC的周长记为p,那么p/BC=2(1-tanβ*tanγ)
2、引理的证明过程如下:
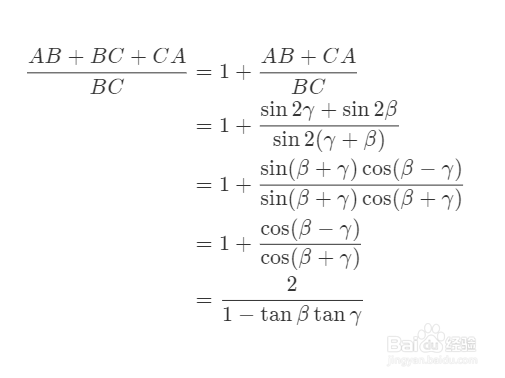
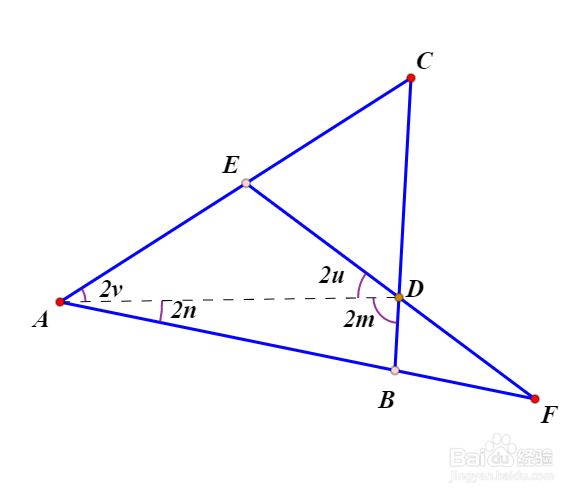
3、回到Urquhart定理:先标注几个角,如下图所示。
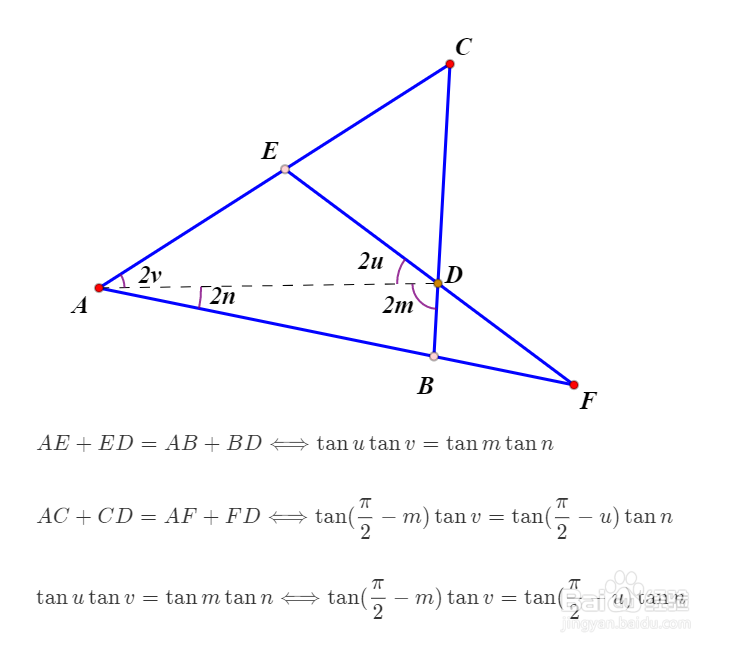
4、因为AE+ED=AB+BD,所以△AED和△ABD的周长相等,且AD是公共边,再结合引理,可以得出如下等价结论。

5、同样的,AC+CD=AF+FD等价条件如下。

6、两个等式右边部分是等价的,所以左边也是等价的。Urquhart定理成立。
1、先介绍一个引理:设△ABC的三个内角是A=2α、B屏顿幂垂=2β、C=2γ,△ABC的周长记为p,那么p/BC=2(1-tanβ*tanγ)

2、引理的证明过程如下:
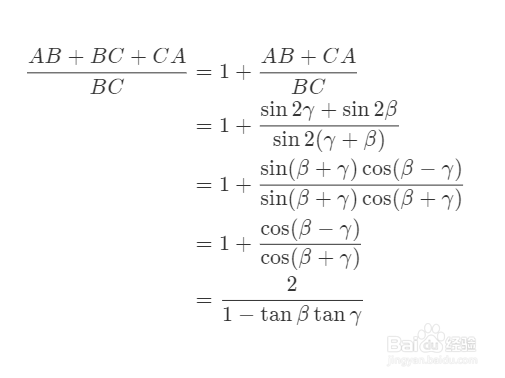
3、回到Urquhart定理:先标注几个角,如下图所示。

4、因为AE+ED=AB+BD,所以△AED和△ABD的周长相等,且AD是公共边,再结合引理,可以得出如下等价结论。

5、同样的,AC+CD=AF+FD等价条件如下。

6、两个等式右边部分是等价的,所以左边也是等价的。Urquhart定理成立。
